최소제곱법 구하기
데이터프레임 만드는 법 <- data.frame((변수1) = c(), (변수2) =c())
c는 벡터 만드는 함수

회귀추정식 만들기
직접 β0(hat) β1(hat) 구해서 [공식에 따라] 회귀직선식 만들거나
model <- lm(반응변수 ~ 설명변수, data = 데이터프레임); model
또는
model <- lm(데이터프레임$반응변수, 데이터프레임$설명변수)

plot 그리기
abline(회귀직선, col = "색깔", lwd = 굵기)

오차분산 추정량 s^2 구하기
1. 구한 회귀진선식에 x를 대입한다
- 직접 식 세워서 넣기
- predict(회귀직선식, newdata = data.frame(temp = 벡터값))

2. residual 잔차 구하기
- 직접 식 구하기
- resid(model) 함수 이용하기
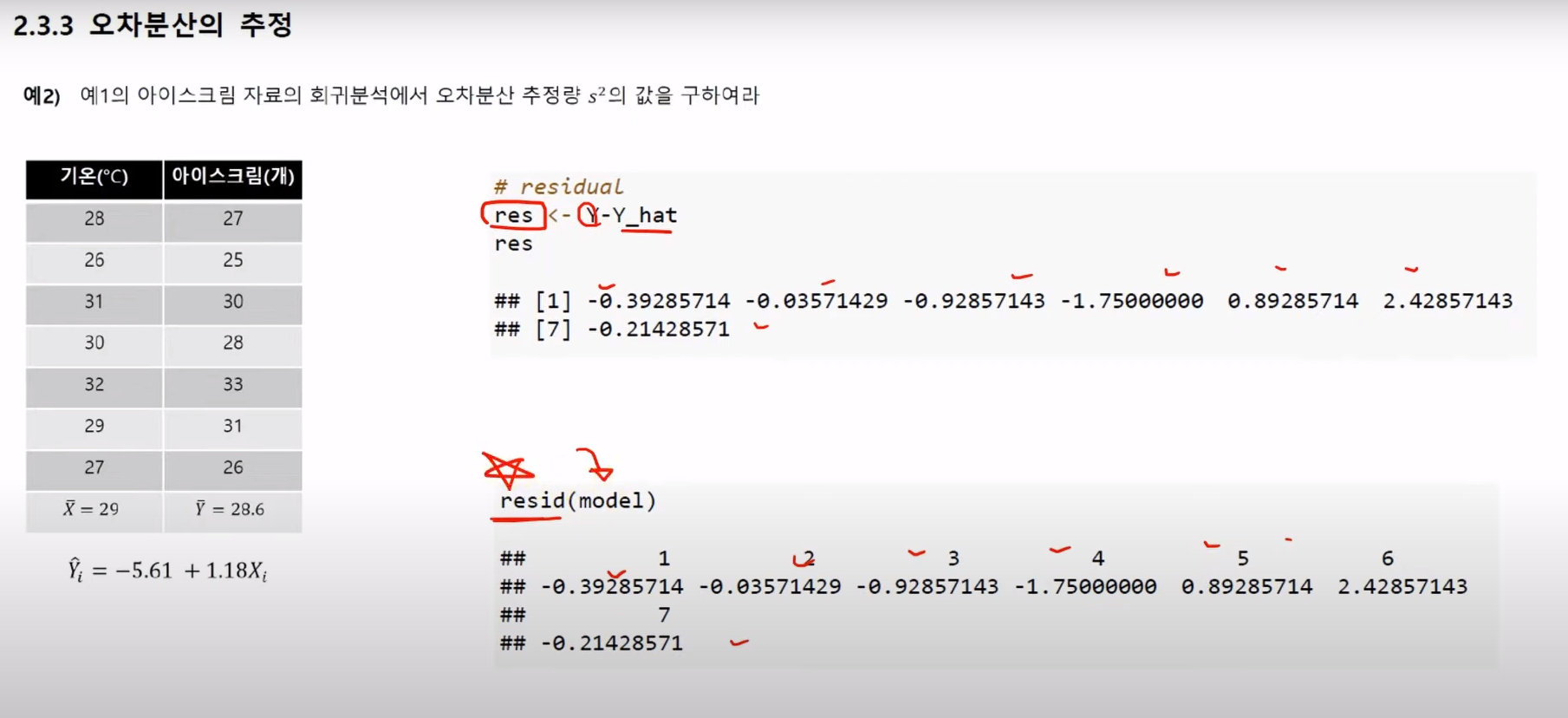
3. 공식에 대입

#Local regression(Loess)
lo_fit <- loess(Y~X, span = 1)
[span은 나눌 넓이의 크기. 좁게 잡으면 울퉁불퉁하게 그려지고 넓게 잡으면 스무스하게 그려짐]
x_loess <- seq(min(X), max(X), (max(X) - min(X))/1000)은 seq(x의 최솟값, x의 최댓값, 쪼갤 간격) 즉 seq는 쪼개기
lo_pre <- predict(lo_fit, x_loess) 쪼갠 값 대입하기
lines(x_loess, lo_pre, col = 'blue', lwd =2)은 lines(x 값, y 값, col = '색깔', lwd = '굵기')
legend("topleft", legend = c("lm", "loess"), col = c("red", "blue"), lty = 1, lwd = 2, cex = 2)은 그래프에 좌측 상단 박스로
legend("위치", legend = c("변수명1", "변수명2"), col = c("red", "blue"), lty = 1은 선, 2는 점선, lwd = 선의 굵기, cex = 박스의 크기)

abline(a = 0, b =1, col = "grey", lwd =2)
abline은 y = a + bx 직선을 그려주는 함수

seq(0,1, by= 0.1)은 0부터 1까지 0.1 간격으로 쪼개기
quantile(A1, prob=seq(0,1,by=0.1))은 quantile(직선식, prob=seq(0,1,by=0.1)) 직선식을 쪼깨서 분위수 구하기
plot(x = Q, y = A1_Q, ylim = c(-5,5), pch = 19, col ="blue", xlab = "probability", ylab = "Fitted values minus Mean")
plot(x벡터, y벡터, ylim = c(y 범위제한), pch = 점 크기, col ="blue", xlab = "probability", ylab = "Fitted values minus Mean")
abline(h = 0, col = "grey", lty = 2, lwd =2)은 h =0 은 가로축으로 ab라인을 그린다는 뜻, lty는 점선, lwd는 굵기


summary(model)이 다 해결

rep(NA,5) 결측치 NA 값을 5번 반복해라 즉 5개 짜리 배열 만들기

for문 이용해서 프레스 값 구하기
for( i in 1:5){
Ice_data_i <- Ice_data[-i, ] 데이터 프레임에서 i번째 뺀 것을 대입
model_i <- lm(Ice~temp, data = Ice_data_i) 회귀모델 만들기
Y_i[i] <- predict(model_i, newdata=data.frame(temp=Ice_data$temp))[i]
i번째 값 대입.
}


R2는 결정계수

1. 공식으로 구하기
2. anova(model) 이용하기
**가 많을 수록 유의수준이 높은 것

'Math > 회귀분석' 카테고리의 다른 글
| [회귀분석] 다중선형회귀분석1 (0) | 2023.03.27 |
|---|---|
| [회귀분석] R를 이용한 회귀계수 추정 (0) | 2023.03.26 |
| [회귀분석] 단순선형회귀분석3 (0) | 2023.03.26 |
| [회귀분석] 단순선형회귀분석2 (0) | 2023.03.19 |
| [회귀분석] 단순선형회귀분석1 (0) | 2023.03.18 |
![[회귀분석] R실습](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbszcjj%2Fbtr4xKstHpn%2FRPOM4DodWkpJpqWbo0G87K%2Fimg.png)