
중선형회귀분석

각 설명변수의 순수한 영향력에 집중하기 위해

예시

선형모형과 비선형모형

행렬을 이용한 모형식


오차항에 대한 기댓값 및 분산 가정

XB는 상수!!

예시

회귀계수의 추정
최소제곱법(OLS)




행렬과 벡터를 이용해 회귀계수 유도
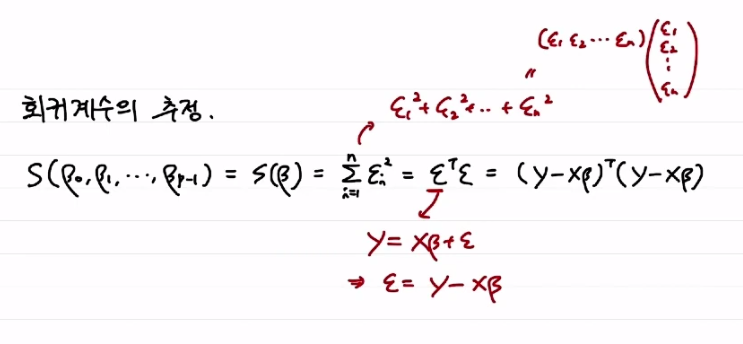

아래처럼 행령의 연산이 스칼라 값이 되면 순서를 바꿔도 같은 값이기 때문에
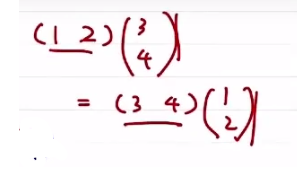
다음과 같이 표현할 수 있다.
2, 3번은 행렬의 미분파트 암기


자유도로 나누어주는 부분에서 빼주는 것은 찾고자하는 계수들의 개수라 생각해도 무방하다.

예제




최소제곱추정량의 성질



비편향 추정량 증명

추정량의 분산 공분산 행렬 증명
X(t)x는 대칭행렬이다.

공분산은 0이 아니다. 존재한다.

가우스 마르코프 정리 BLUE

1번과 3번에 대한 증명. 2번은 위에서 증명함
1번 증명 이걸로 끝

3번 증명
B(hat)*을 가정하기 D를 추가


행렬의 분산 공식 참고

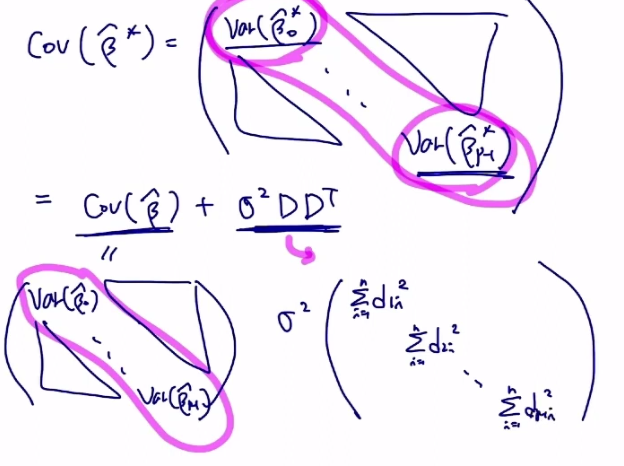
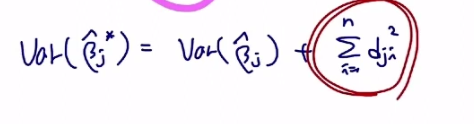
그 외 유용한 사실들

1. 잔차들의 합이 0이다. (증명)

오차항들의 합은 0이다
x와 오차항은 서로 독립이다.
x와 오차항들의 가중합은 0이다

2. 잔차들의 x_j에 대한 가중합은 0이다. (증명)


3. 잔차들의 y(hat)_j에 대한 가중합은 0이다. (증명)
H는 멱등행렬의 성질을 가지고 있다.
H는 대칭행렬의 성질을 가지고 있다.


4. 적합된 회귀식은 (X_1(평균), ... , X_p-1(평균), Y(평균))을 지난다.


'Math > 회귀분석' 카테고리의 다른 글
| [회귀분석] 중회귀분석에서의 적합도와 분산분석 (0) | 2023.03.27 |
|---|---|
| [회귀분석] R을 이용한 중회귀분석 회귀계수 추정 (0) | 2023.03.27 |
| [회귀분석] R를 이용한 회귀계수 추정 (0) | 2023.03.26 |
| [회귀분석] 단순선형회귀분석3 (0) | 2023.03.26 |
| [회귀분석] R실습 (0) | 2023.03.19 |
![[회귀분석] 다중선형회귀분석1](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FNdhbi%2Fbtr5TouI3qE%2FAAAAAAAAAAAAAAAAAAAAAE9eRSj3F41wj5x_DOvlWp7R8jEp-p1SE2meO0DABubG%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1753973999%26allow_ip%3D%26allow_referer%3D%26signature%3DOUBRmpraRDhbJRC5tTLZ%252BhaVeFM%253D)