5.9 Enhancing Parallelism(병렬성 향상시키기)
- 이 시점에서 우리의 기능은 산술 unit의 latency에 의한 한계에 도달했다.
- 그러나 덧셈과 곱셈을 수행하는 functional unit은 모두 fully pipelined으로 되어 있다. 이는 매 clock cycle 마다 새로운 operation을 시작 할 수 있으며, 일부 operation은 여러 functional unit에서 수행될 수 있는 것을 의미한다.
- 하드웨어는 더 높은 속도로 곱셈과 덧셈을 수행할 수 있는 잠재력을 가지고 있지만, 우리 코드는 단일 변수 acc로 값을 축적하고 있기에(루프 언롤링으로 성능 향상 불가) 이 기능을 활용할 수 없다. 이전 계산이 완료될 때까지 acc에 대한 새 값을 계산할 수 없기 때문이다.
- acc에 대한 새 값을 계산하는 기능 장치가 매 clock cycle마다 새 operation을 시작할 수 있지만, L(latency) cycle 마다 하나만 시작하기 때문에 기능을 더 높은 속도로 수행할 수 없다.
- 이 다음부터는 순차적인 종속성을 부수고 병렬성을 이용하여 latency bounds를 향상시키는 방법에 대해 알아볼 것이다.
5.9.1 Multiple Accumulators
- integer 덧셈이나 곱셈과 같이 associative하고 commutative한 결합 연산의 경우 결합 연산 집합을 두 개 이상의 부분으로 나누고 마지막 결과를 결합하여 성능을 향상시킬 수 있다. (분할하여 계산)

- 예를 들어, Pn이 원소 a0, a1, ... an-1의 곱을 나타낸다고 가정하자.
- n이 짝수이면 이 식을 Pn = PEn * POn으로 쓸 수 있다. PEn은 짝수 지수를 가진 원소의 곱이고, POn은 홀수 지수를 가진 원소의 곱이다.
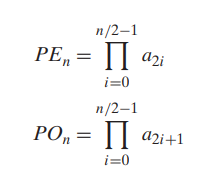
- 아래 코드는 위 방법을 사용한 것이다.
/* 2 x 2 loop unrolling */
void combine6(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc0 = IDENT;
data_t acc1 = IDENT;
/* Combine 2 elements at a time */
for (i = 0; i < limit; i+=2) {
acc0 = acc0 OP data[i];
acc1 = acc1 OP data[i+1];
}
/* Finish any remaining elements */
for (; i < length; i++) {
acc0 = acc0 OP data[i];
}
*dest = acc0 OP acc1;
}
- 코드를 보면, 반복당 더 많은 요소를 결합하기 위해 양방향 루프 언롤링과 양방향 병렬화를 모두 사용하여 변수 acc0의 짝수 인덱스를 가진 요소와 변수 acc1의 홀수 인덱스를 가진 요소를 누적하는 방식이다.
- 우리는 이것을 2 * 2 루프 언롤링이라 부른다.
- 이전과 마찬가지로 벡터의 길이가 2의 배수가 아닌 경우에 대해 나머지 array요소를 축적하기 위한 두 번째 루프가 포함된다.
- 그 후 acc0 및 acc1 결합 연산을 적용하여 최종 결과를 계산한다.
- one-way 에서 two-way 루프언롤링 방식을 이용하면 다음과 같은 결과가 나온다.
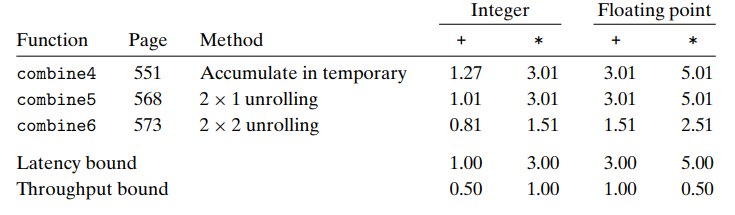
- integer 곱, floating point(부동 소수점) 덧셈 및 부동 소숫점 곱셈이 약 2배 향상되고 정수 덧셈도 다소 개선되는 결과를 보여준다. 모든 경우에 대해 성능이 향상되었다.
- 이는 latency bound의 한계를 부순 것이다.
- 프로세서는 순차적으로 수행하지 않고 병렬적으로 operation을 수행해서 성능을 향상시킬 수 있다.
Combine6 그래프화
- 아래 그림은 combine6을 그래프화 시킨 것이다.
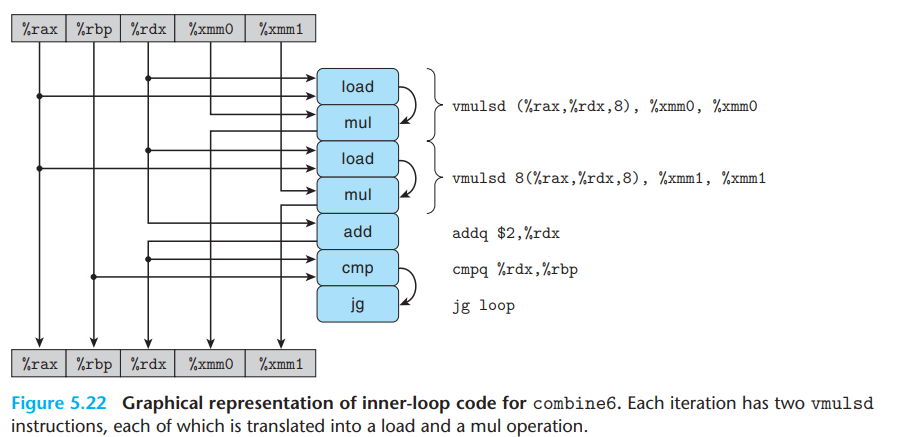
- 아래 그림은 표시된 프로세스 통한 반복 간의 데이터 종속성을 보여주는 템플릿이다.
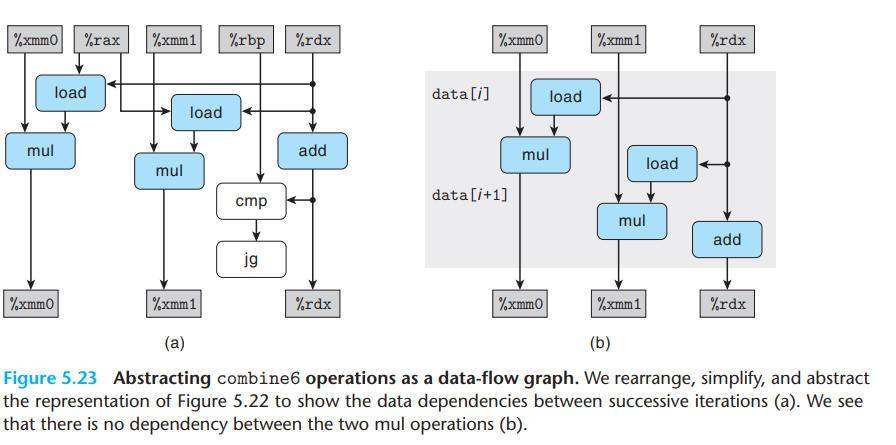
- combine5와 마친가지로 내부 루프에는 두 개의 vmulsd 작업이 포함되어 있지만, 이러한 방식은 별도의 레지스터를 읽고 쓰는 mul operations으로 해석되고 이들 사이에 데이터 종속성은 없다. 위 그림 (b)
- 이 템플릿을 n/2회 복제하여 길이 n의 벡터에서 함수의 실행을 모델링하면 다음과 같다.

- 우리는 이제 짝수 번호 요소 (acc0)의 곱을 계산하고 홀수 번호 요소 (acc1)에 해당하는 두 개의 critical path가 존재함을 알 수 있다.
- 이러한 각 critical path는 n/2 operation만 포함되므로 CPE 는 약 5.00/2 = 2.50이다. CPE가 L/2로 줄었다.
- 하지만 이것만으로는 1.0 CPE로 이론적 한계인 0.50 CPE에 도달하지 못했다. 루프의 오버헤드가 아직 많기 때문이다.
- k 요소만큼 루프 언롤링하고 k 값을 병렬로 누적하여 k * k 루프를 생성하도록 Multiple Accumulators를 일반화 가능하다.

- 위 그림은 k =10까지의 값에 대해 Multiple Accumulators 변환을 적용하는 효과를 보여준다.
- 충분히 큰 k에 도달하면 모든 경우에 대해 처리량 한계에 거의 도달한다.
- 일반적으로 모든 functional unit에 대해 파이프라인을 채워 유지할 수 있는 경우에만 throughput bound를 달성할 수 있다.
- latency L과 capacity C에 대한 operation의 경우, k ≥ C * L의 언롤링 계수가 필요하다.
- 예를 들어, 부동 소수점 곱셈은 C =2, L = 5이므로 k ≥ 10이 필요하다. 부동 소수점 덧셈은 C = 1이고 L = 3이므로 k ≥ 3으로 throughput bound에 달성한다.
- k * k 언롤링 변환을 수행할 때, 함수의 기능이 그대로인지 확인해봐야한다.
- 정수 데이터의 경우 2의 보수를 이용(commutive, associative 함)하기 때문에(chapter 2 참고), 정수 데이터 유형의 경우 가능한 모든 조건에서 combine6와 combine5의 계산된 결과는 같다.
- 따라서 최적화 컴파일러는 combine4에 표시된 코드를 루프 언롤링을 통해 combine5의 two-way 언롤링으로 변환시킨 후 병렬 처리를 도입하여 combine6 코드로 변환할 수 있다.
- 반면, 부동 소수점 데이터의 경우 곱셈과 덧셈은 서로 연관성이 없다. 따라서 combine5와 combine6는 반올림 또는 오버플로우로 인해 서로 다른 결과가 도출될 수 있다.
- 예를 들어, 짝수 지수를 가진 모든 원소가 절대값이 매우 큰 숫자인 반면, 홀수 지수를 가진 원소는 0.0에 매우 가깝다는 곱 계산이 이루어지면 PEn이 오버플로우 되거나 POn이 언더플로우 될 수 있다. 실제론 데이터가 연속적이기 때문에 이럴 가능성이 낮다. 심지어 결과도 두 그룹으로 독립적으로 곱한 것이 더 정확도가 높을 것이다.
- 그러나 컴파일러는 이러한 위험 요소를 판단할 수 없기 때문에, 부동 소숫점 데이터에서 해당 변환을 수행하지 않는다.
5.9.2 Reassociation Transformation
- 순차적 종속성의 한계를 깨고 성능을 향상시킬 또 다른 방법은 Reassociation Transformation이다
- 단순히 코드를 아래와 같이 변환시켜도 성능이 크게 향상될 수 있다.
acc = (acc OP data[i]) OP data[i+1];↓
acc = acc OP (data[i] OP data[i+1]);
- 두 개의 괄호를 배치하는 방식에만 차이가 존재한다.
- 이를 Reassociation Transformation 재연관 변환이라 한다.
- 괄호가 벡터 요소가 누적되는 값인 acc와 결합되는 순서를 바꿔 2 * 1a라 불리는 루프 언롤링 형태를 도출한다.
- 정수 덧셈의 경우, k * 1 언롤링(combine5) 성능과 일치하는 반면, 나머지 세 가지 경우는, Multiple Accumulators(combine6)의 버전의 성능과 일치하여 k * 1 언롤링에 비해 성능이 두배가 된다. 순차적 종속성의 한계를 를 깼다.
- 아래 그림 참고

- 아래 코드는 combine7의 내부 루프에 대한 코드가 연산 및 데이터 종속성 결과로 디코딩되는 방법을 보여준다.
- vmovsd와 첫 번째 vmulsd 명령에 따른 load operation은 메모리에서 벡터 요소 i와 i + 1을 로드하고 첫 번째 mul operation은 이를 함께 곱한다.
- 두 번째 mul operation은 이 결과에 누적 값 acc를 곱합니다.
/* 2 x 1a loop unrolling */
void combine7(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc = IDENT;
/* Combine 2 elements at a time */
for (i = 0; i < limit; i+=2) {
acc = acc OP (data[i] OP data[i+1]);
}
/* Finish any remaining elements */
for (; i < length; i++) {
acc = acc OP data[i];
}
*dest = acc;
}- 아래 그림 5.27의 operation을 재정렬, 세분화, 추상화하면, 5.28 (a), (b)가 도출되어 한번의 반복에 대한 데이터 종속성을 나타낼 수 있다.


- 우리는 두 개의 load operation와 두 개의 mul operation 가지고 있지만, mul operations 중 하나만이 루프 레지스터 간의 데이터 종속 chain을 형성한다.
- 그림 5.29는 위 템플릿을 n/2번 반복하여 n개의 벡터 요소를 곱하는 데 수행된 계산을 보여준다.
- n/2 개 operation이 critial path에 존재하고 각 반복 내의 첫번째 곱셈은 이전 반복에서 누적된 값을 기다리지 않고 수행할 수 있다.
- 따라서 CPE를 최소 약2배까지 줄일 수 있다.
- 아래 그림은 k = 10까지에 대해 k * 1a 루프 언롤링을 이루기 위해 Reassociation Transformation 재결합 변환을 적용한 결과이다.

- 이 변환은 k * k 언롤링으로 k개의 별도 accumulator을 유지함으로써 달성되는 것과 유사한 성능 결과를 낸다.
- 정수 데이터의 경우 Reassociation Transformation 후 결과가 동일하지만, 부동 소숫점 데이터의 경우 Reassociation Transformation 후 결과가 달라질 수 있는지 확인해야한다.
- 대부분의 컴파일러는 Reassociation Transformation을 부동 소숫점 데이터의 경우 수행하지 않는다.
'Computer Science > 컴퓨터 구조' 카테고리의 다른 글
| [CSAPP] 5.11 Some Limiting Factors(일부 제한 요인들) (0) | 2023.02.08 |
|---|---|
| [CSAPP] 5.10 Summary of Results for Optimizing Combining Code (최적화 코드의 결과 요약) (0) | 2023.02.08 |
| [CSAPP] 5.8 Loop Unrolling(루프 풀기) (0) | 2023.01.30 |
| [CSAPP] 5.7 Understanding Modern Processors(현대 프로세서 이해) (0) | 2023.01.30 |
| [CSAPP] 5.6 Eliminating Unneeded Memory References(불필요한 메모리 참조 제거) (0) | 2023.01.30 |
![[CSAPP] 5.9 Enhancing Parallelism(병렬성 향상시키기)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FQhA5t%2FbtrXA9k8Gw9%2FqjnIvknQ7f45qckSZJmVa1%2Fimg.png)