2.3 Integer Arithmetic(정수 연산)
- 많은 프로그래머들은 두 개의 양의 정수를 더 할 때 음수 값이 나오거나 x<y, x-y<0 값이 다르게 나오면 놀란다.
- 컴퓨터 산술연산의 원리를 이해하면 이 문제를 이해할 수 있다.
2.3.1 Unsigned Addition(비부호형 덧셈)

- 비부호형 덧셈 연산자, u는 unsigned 의미 w는 bit 수
- 두 개의 0 포함 양의 정수 x,y, 0≤x, y≤2^w 라 가정, 두 합의 계산 범위는 0≤x+y≤2^(w+1)-2이다. 따라서 두 합의 크기를 표현 하기 위해서는 w+1개의 비트가 필요하게 된다.
- 즉 산술연산 결과를 완벽하게 표시하려면 필요한 워드 크기를 제한할 수 없다.
- 그러나 대부분의 프로그래밍 언어들은 고정길이 산술연산을 지원한다. 따라서 “덧셈”과 “곱셈”같은 연산은 정수에 대한 일반적인 연산들과는 다르다.
- x,y에 대해 x+y 정수합을 w비트 길이로 절삭한 후에 다시 비부호형 정수로 나타낸다. (데이터 크기가 계속 확장되는 것을 방지하기 위해)
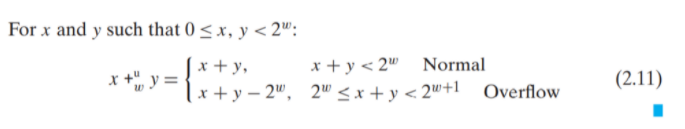
- Normal case의 경우 x+y w비트 패턴 내 표현 가능, But Over flow case의 경우 w+1 bit pattern이 1이므로 해당 비트를 버리는 것은 sum에서 2^w를 빼는 것과 같다.

- Overflow란 데이터 타입의 제한된 워드 사이즈 범위를 벗어나서 산술연산의 결과를 표현할 수 없는 것을 의미

Detecting overflow of unsigned addition

Derivation: Detecting overflow of unsigned addition

Unsigned negation(음수부호화)

Two’s-Complement Addition(2의 보수 덧셈)
- 2의 보수 덧셈 연산의 결과가 매우 크거나 매우 작아서 표현할 수 없을 때 연산 결과


- 2의 보수의 덧셈 연산의 결과가 2^(w-1) 이상이라면 양의 Overflow라고 하며 합 결과에 2^w를 빼준다.
- 2의 보수의 덧셈 연산의 결과가 -2^(w-1) 미만이라면 음의 Overflow라고 하며 합 결과에 2^w를 더해준다.

Example
Detecting overflow in two’s-complement addition
2.3.3 Two’s-Complement Negation(2의 보수 음수부호화)

- TMinw = -2^(w -1) (표현할 수 있는 최소값) ex) 100…000
- TMaxw = 2^(w -1) -1 (표현할 수 있는 최댓값) ex) 011…111

2.3.4 Unsigned Multipliacation(비부호형 곱셈)
Unsigned Multiplication
- Unsigned integer의 곱셈에 관한 것이다.
- unsigned integer x, y가 있는데 0~2^w-1이면 w 비트로 표현할 수 있다.
- 하지만 x*y는 (2^w-1)^2이니 2w 비트보다 더 많이 필요할 수 있다.
- int가 4바이트인데 x*y도 int로 저장해야 할 것이다.
- 그런데 4바이트 * 4바이트하면 8바이트가 되어서 int에 저장을 못하게 된다.
- 그래서 아래의 방법을 사용하는 것이다.
- 대신에 C에서 unsigned integer 곱셈은 결과로 나온 2w 비트의 하위 w 비트에 의해 값이 나오게 정의되었다.
- w비트를 잘라내는 것은 2^w로 나머지 연산하는 것과 같은 효과다.

2.3.5 Two's-complement Multiplication(2의 보수 곱셈)
two’s-complement multiplication
- 역시 w bit 정수를 2의 보수로 표현한 값들을 곱하면 2w bit가 필요하게 된다.
- 역시 여기도 하위 w bit만 저장하는 것이다.
- 이렇게 하면 결과가 x*y를 2^w로 나머지 연산한 것을 unsigned에서 2의 보수로 바꾼 값과 같게 나온다.

- 2의 보수로 바꾸는 것은 부호를 바꿔주는 것이다.
- 비트에서는 0을 1로, 1을 0으로 바꾸고 뒤에 1만 추가해주면 된다.
- 101 이라는 값이 있으면 010으로 바꾸고 011하면 되는 것이다.

- 그래서 이 예제를 보면 unsigned로 하면 x는 101이니 5이다.
- 그래서 x*y=15, 2^w= 8. 왜냐하면 3비트로 표현하고 있기 때문에
- 그러면 (x*y) mod 8 = 7이다.
- 7을 3 bit로 표현하면 111이다. 이것을 2의 보수로 읽으면 -1이다.
- 그래서 보면 bit 연산에서 unsigned 곱셈과 2의 보수 곱셈은 같은 값을 가지는 것을 알 수 있다.
- 6bit로 계산한 것들은 다른 값을 가져도 3bit로 자르고 나면 같은 2진수를 가진다.
- 하지만 unsigned로 읽냐 2의 보수로 읽냐에 차이로 10진수에서 차이가 나는 것이다.

2.3.6 Multiplying by constants(상수를 사용한 곱셈)
Multiplying by constants
- integer multiply 명령어는 다른 더하기, 빼기, bit 연산자들보다 느리다.
- 곱셈 명령어는 10 clock cycle이 도는데 다른 것들은 1~3 clock cycle 정도 걸린다고 한다.
- 그래서 컴파일러에서 중요하게 사용되는 최적화에는 곱셈을 shift 연산과 덧셈 연산으로 바꾸는 것이 있다고 한다.
- 곱셉을 2의 제곱으로 하는 것이 있다.
- unsigned integer w bit 숫자 x가 있다고 할 때 여기에 k bit를 더하면 결과는 x*2^k가 된다.
- 뒤에 k개의 0을 더 붙이는 것이다.
- 11을 이진수로 하면 1011인데 여기에 뒤에 2 bit를 추가하면 101100이 된다.
- 101100은 32+8+4=44이다. 즉 114 = 112^2인 것이다.
- integer multiply 명령어는 다른 더하기, 빼기, bit 연산자들보다 느리다.
- 곱셈 명령어는 10 clock cycle이 도는데 다른 것들은 1~3 clock cycle 정도 걸린다고 한다.
- 그래서 컴파일러에서 중요하게 사용되는 최적화에는 곱셈을 shift 연산과 덧셈 연산으로 바꾸는 것이 있다고 한다.
- 곱셉을 2의 제곱으로 하는 것이 있다.
- unsigned integer w bit 숫자 x가 있다고 할 때 여기에 k bit를 더하면 결과는 x*2^k가 된다.
- 뒤에 k개의 0을 더 붙이는 것이다.
- 11을 이진수로 하면 1011인데 여기에 뒤에 2 bit를 추가하면 101100이 된다.
- 101100은 32+8+4=44이다. 즉 114 = 112^2인 것이다.
- 만약에 k bit로 고정되어 있는데 뒤에 더 추가되면 앞의 bit들은 버리게 되는 것이다.
- 이것은 k bit로 고정되어 있을 때 그냥 곱셈 명령어 해도 똑같이 된다.
- 그래서 그냥 똑같이 bit 뒤에 추가하면 된다.
- 2의 보수도 역시 unsigned와 같은 결과를 가지니 곱셈을 2의 제곱으로 즉 shift 연산으로 할 수 있다.
- unsigned와 2의 보수 곱셈 모두 overflow가 일어날 수 있다.
- shift 연산으로 해도 역시 overflow가 일어날 수 있다.
- 그래서 넘어가는 비트를 자르는데 결과 값은 위에서 한 것처럼 나머지 연산한 결과가 나온다.
- 곱셈 연산은 비용이 많이 들어서 많은 C 컴파일러는 곱셈을 shift 연산자나 더하기 빼기로 상수와 곱셈하는 것을 바꾸려고 한다.
- 예를 들어 x*14 이런 것이 있으면 14가 1110이니 (x<<3) + (x<<2) + (x<<1)로 바꾸려고 한다.
- 2의 보수일 때도 똑같이 한다.
- 아니면 14 = 2^4 − 2^1 이니 (x<<4) - (x<<1) 이렇게 바꿀 수 도 있다.
- 이진수에서 1이 연속적으로 나오는 경우 아래와 같이 바꿀 수 있다.
- 이 때 n은 1이 가장 처음 나오는 부분의 index이고 m은 마지막으로 나온 index이다.

- 위의 예시에서 14가 1110이니 (x<<3) + (x<<2) + (x<<1) or (x<<4) - (x<<1)로 바뀌는 것이다.
- 이렇게 곱셈을 shift와 덧셈, 뺄셈으로 대체할 수 있는데 이 둘의 속도를 비교해서 할 것이고 이것은 machine dependent하다.
- 덧셈이나 뺄셈이 매우 많아지면 곱셈이 더 빠를 것이다.
- 그래서 대부분 컴파일러는 이 최적화는 적은 수의 shift나 덧셈, 뺄셈일 때만 한다.
- 컴파일러가 위에서 덧셈을 쓸 것인가 뺄셈을 쓸 것인가를 어떻게 결정하는가 하면 n=m 이거나 n=m+1인 경우 덧셈을 사용한다.
- 하지만 n>m+1인 경우 뺄셈을 사용한다.
- 왜냐하면 n=m이면 덧셈은 shift 한번, 뺄셈은 shift 두번 한다.
- n=m+1이면 둘 다 shift 두번 한다.
- 하지만 n>m+1이 되면 뺄셈은 shift 두번하지만 덧셈은 n-m+1번 shift 필요한데 이것은 2보다는 항상 크다.
2.3.7 Dividing by Powers of 2(2의 제곱으로 나눗셈하기)
dividing by powers of 2
- 정수 나눗셈은 대부분의 machine에서 곱셈보다 더 느리다.
- 30이상 clock cycle이 필요하다고 한다.
- 나눗셈도 shift 연산으로 할 수 있다고 한다.
- 곱셈은 left shift를 했는데 나눗셈은 right shift를 한다고 한다.
- 이렇게 right shift하게 되면 2의 거듭 제곱으로 나누고 0의 자리로 반올림하는 것과 같다.

- 정수 나눗셈은 항상 0을 향해 반올림한다.

- 이 기호는 내림이다.

- 이 기호는 올림이다.
- 그래서 x≥0, y>0일 때 정수 나눗셈은 아래와 같다.

- 하지만 x<0, y>0일 때 정수 나눗셈은 아래와 같다.

- 결과가 양수면 버림하는데 음수면 올림한다는 것이다.
- 이것이 필요한 이유는 unsigned는 양수이고 2의 보수는 음수도 있기 때문이다.
- unsigned 정수의 나눗셈은 right shift로 할 수 있다.
- unsigned 정수의 경우 x>>k는 아래와 같은 결과를 얻는다.

- 이것이 unsigned 정수를 right shift한 결과다.
- 0의 자리에서 내림하면 실제 값과 동일하게 나오는 것을 볼 수 있다.

- x가 w bit일 때 앞에서부터 w-k bit만큼 자른 것이 x’, 나머지 k bit이 x’’라고 하면 x=2^k*x’+x’’다.
- 이때 x’’는 k bit이니 0이상 2^k미만이다.
- 따라서 x를 2^k로 나누면 x/2^k=x’ + x’’/2^k이다.
- 이때 x’’/2^k는 0이상 1미만이기 때문에 내림하면 x’가 된다.
x:

x’:
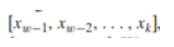
x’’:

- 그래서 k bit만큼 right shift하면 x/2^k를 내림한 결과가 나오는 것이다.
- 2의 보수를 2의 거듭 제곱으로 나누는 것은 조금 더 복잡하다 .
- 음수가 유지될 수 있게 arithmetic right shift를 써야 한다고 한다.
- right shift에는 arithmetic, logical 2가지 종류가 있다.
- logical은 그냥 0을 채워 넣는 것이다.
- arithmetic은 sign bit가 복제되어 그것을 채워 넣는 것이다.

- 위가 arithmetic shift이고 아래가 logical shift이다.
- 그래서 2의 보수를 2의 거듭 제곱으로 나눌 때 즉 right shift를 할 때 2의 보수가 양수 였다면 sign bit가 0이기 때문에 arithmetic shift가 logical shift와 같은 효과를 낸다.
- 그래서 양수인 경우 위와 같이 똑같이 하면 되는 것이다.
- 하지만 음수인 경우 다르다.
- 음수이니 arithmetic shift를 하게 되면 10진수 값이 아래와 같이 나온다.
- 하지만 2의 거듭 제곱으로 나눈 값을 보면 내림을 해야 10진수의 값이 나온다.
- 음수일 때는 올림을 해야 한다고 했는데 그냥 arithmetic shift를 하면 내림하는 상황이 생긴다.

- 이렇게 반올림이 적절하지 않은 것을 shift하기 전에 bias를 추가함으로써 고칠 수 있다.
- k만큼 shift한다고 하면 (x + (1<<k) -1)="">> k 하면 arithmetic shift하면 x/2^k를 올림한 결과와 같이 나온다는 것이다.

- 여기서 (1<<k) -1의 의미는 만약에 k가 4라고 하면 1111을 더하는 것이다.
- 이렇게 bias를 더하면 위의 bit에 증가를 일으켜서 결과가 0을 향해 반올림 되는 효과를 가져온다고 한다.
- 그래서 아래와 같은 식이 만족함을 할 수 있다.

2.3.8 Final Thoughts on Integer Arithmetic
final thoughts on integer arithmetic
- 여기까지 본 것은 컴퓨터에서 정수 연산은 나머지 연산의 형태였다는 것이다.
- 또 수를 표현하기 위해 고정된 길이를 사용해서 값에 범위가 있고 이것이 overflow를 일으킬 수 있다는 것이다.
- 또 2의 보수 표현으로 양수, 음수를 잘 표현하고 unsigned나 2의 보수 표현 모두 연산할 때 똑같거나 비슷한 비트 level에서 행동을 보인다는 것을 알았다.
- 이런 것들은 찾기, 이해하기 어려운 버그의 원천이 될 수 있다.
'Computer Science > 컴퓨터 구조' 카테고리의 다른 글
| [CSAPP] 3.1 A Historical Perspective(역사적 관점) (0) | 2023.01.21 |
|---|---|
| [CSAPP] 2.4 Floating Point(부동소수점) (0) | 2023.01.19 |
| [CSAPP] 2.2 Integer Representations(정수의 표시) (0) | 2023.01.19 |
| [CSAPP] 2.1 Representing and Manipulating Information(정보의 저장) (1) | 2023.01.19 |
| [CSAPP] Computer Systems A Programmer's Perspective: 컴퓨터 구조 책 추천 (0) | 2023.01.17 |
![[CSAPP] 2.3 Integer Arithmetic(정수 연산)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F6JXo6%2FbtrWI12GQmW%2FAjbxZtlHkKZk64b1Ffz0q0%2Fimg.png)