학습 주제
- 정보의 표현
정리한 내용
개요
Two-valued signals
- 종류
- punched card의 hole의 존재 유무
- wire의 high or low voltage
- 시계방향과 반시계방향의 자기장 domain
- 장점
- 저장과 계산에 대한 전자 회로가 간단하다.
- 수백만, 수십억개의 회로를 하나의 silicon chip에 통합할 수 있다.
학습 방식
- 수와 다른 형태의 data들이 어떻게 computer에서 표현되는지를 알아볼 것이다.
- 이 data들에 대해 컴퓨터가 동작하는 연산들의 특징들을 알아볼 것이다.
- 수학적인 언어와 공식 및 방정식을 작성하고 중요한 성질을 유도하는 것이 필요하다.
- 처음에는 수학적으로 나타내고, 이후 예시와 여러 의견들을 보며 설명할 것이다.
2.1 Information Storage
<aside> 💡 C 프로그램 언어의 역사
Bell Lab에서 Unix Operating system을 위해 C언어가 개발되었다.
1989: Bell Lab C가 ANSI C Standard를 이끌었다. (표준화가 이때부터 진행됨) - 함수가 선언되는 방식
1990: ISO 90 (ANSI C in 1990과 동일)
1999: ISO 99 - 새로운 data type들과 비영어권의 문자들을 필요로하는 text string들을 지원
2011: ISO 11 - 추가적인 data type들과 여러 특징들을 포함 - backward compatible을 만족하도록 함 (새로운 표준을 따르는 compiler로 compile을 한 프로그램은 이전 표준을 따라 작성된 프로그램과 동일한 동작을 수행해야 함
GCC: GNU Comiler Collection, option으로 원하는 버전의 표준으로 compile을 수행할 수 있다.
- -std=c11 : ISO 11버전으로 compile
- -ansi : -std=c89 와 동일한 효과 (c90을 c89라고 하기도 한다. 프로젝트 를 시작한 날짜가 89년도이기 때문에)

2.1.1 Hexadecimal Notation
why 16진수?
- 10진법은 bit pattern을 설명하기 불편하다.
- bit pattern을 확인할 때 2진법은 너무 길다.
📖 위와 같은 이유 때문에 비트 패턴은 4비트로 묶어 보는 것이 편하다. 예를들어
0100 1000 0010 1111 이것을 16진수 명명법으로 나타낸다면 단순하게 각 4비트를 묶어서 16진수 482F로 변환하면 된다.
0100 1000 0010 1111 = 4 8 2 f
- C에서는 영문자는 대문자 또는 소문자, 심지어 혼용하는 것도 허용한다.
- $x = 2^n$ 꼴의 수일 경우의 hex 표현
- 하나의 hex digit을 제외한 나머지 n개는 0으로 채워진 bit로 표현된다
- 2의 지수(n)을 i + 4j 꼴로 나타낼 수 있다.
- i = 0 → hex digit = 1
- i = 1 → hex digit = 2
- i = 2 → hex digit = 4
- i = 3 → hex digit = 8
- 따라서 2048의 hex 표현은 0x800이다.
2.1.2 Data sizes
word size
- register의 size
- virtual address에서 encoding되는 단위
- virtual address space의 maximum size를 결정짓는 요소
- w-bit word size를 가지는 machine에서는 0 ~ 2^{w-1} bytes의 범위를 가진다.
32-bit machine and 64-bit machine
- compile : backward compatibility에 의해 64-bit machine에서도 32-bit program으로 돌릴 수는 있다.
- gcc -m32 prog.c
- 즉, 32-bit program과 64-bit program은 어떤 machine에서 실행되는지가 아닌, 어떻게 compile되었는가에 따라 나뉜다.
integer data size
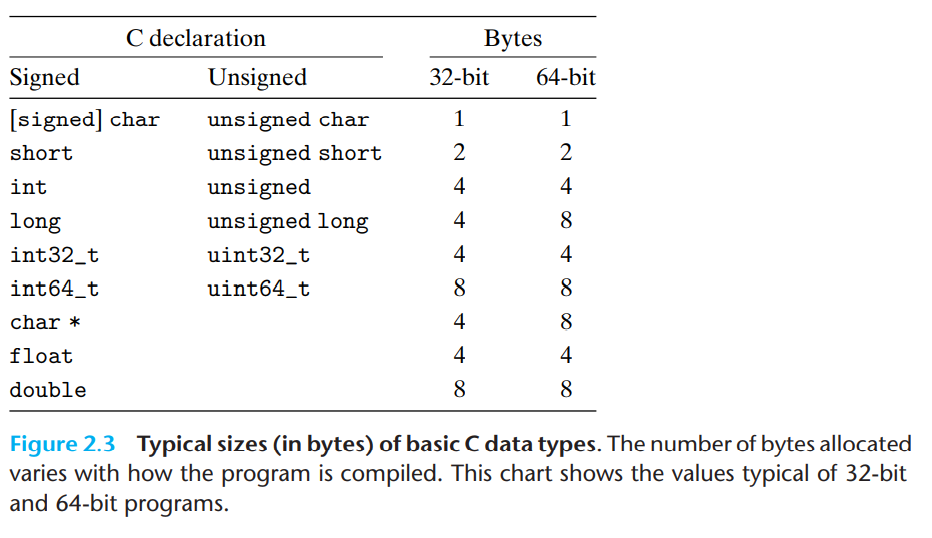
- 32-bit program과 64-bit program에서 data size가 다르다.
- Typical size : 보장되는 size와는 다르게 보장이 되지 않는 size들이다.
- machine마다 달라질 수 있다.
- 운영체제마다 달라질 수 있다.
- compiler setting에 따라 달라질 수 있다.
- 이러한 typical size을 피하는 방법으로 fixed size를 사용하는 것이 있다.(예. int32_t나 int64_t 타입들)
- 다양한 machine과 compiler들에 portable(이식가능)하도록 노력해야 한다.
- 보통 C에서는 integer와 관련있는 data type들에선 하한을 정해둔다.
- 딱 이 size를 갖는다는 명세는 없고, 적어도 이정도의 size는 가져야 한다는 명세가 있다.
- 32-bit program에선 int type으로 pointer를 관리할 수 있었는데, 64-bit program에선 문제가 될 수 있다.
- 1980 ~ 2010년또까지 주로 32-bit machine을 사용해왔고, 그 이후부턴 64-bit machine을 주로 사용한다.
- C언어 표현의 관대함
- 이 표현들은 모두 동일한 의미를 가진다.

pointer data size
- full word size를 가진다.
floating-point formats data size
- single-precision(float) : 4byte
- double-precision(double) : 8byte
2.1.3 Addressing and Byte Ordering
- 단일 byte가 아닌, multi-byte를 저장해야 할 때 두가지를 정해야 한다.
- 해당 data가 어느 주소에 있을지
- memory에서 어떻게 이 byte들을 ordering할 지
little endian & big endian
※ 여기서 말하는 MSB, LSB의 B는 Byte를 의미한다.(bit가 저장되는 순서는 하나의 byte안에서는 모두 동일하다)
- bit endian : 낮은 주소에 MSB부터 저장한다.
- memory에 저장된 순서 그대로 읽을 수 있어서 이해하기에 더 쉽다.
- little endian : 낮은 주소에 LSB부터 저장한다.
- 산술 연산시에 효율적이라고 한다.
- 예시 - 0x012345678을 저장할 때

bi-endian
- 요즘 processor chip은 bi-endian이다. 이는 little 또는 bit endian으로 설정이 가능하다는 뜻
- 하지만 hardware는 설정할 수 있는 bi-endian이지만, OS에선 한가지 byte-ordering mode를 정한다.
왜 endian을 알아야 하는가?
- 보통의 경우 programmer 입장에선 이 endian이 감춰져 있으므로 신경쓰지 않아도 된다.
- 하지만 다음과 같은 경우 신경을 써야 한다.
- network를 통해 binary data를 주고 받을 경우
- 문제가 되는 상황은 little endian과 big endian machine 사이에서의 통신일 때 발생한다.
- 한쪽에서 big-endian으로 된 data를 보냈는데, little-endian으로 해석하게 되면 data가 달라지기 때문
- machine-level program을 검사할 때
- unsigned char *로 casting을 할 때 → casting되는 type을 byte sequence로 보려고 할 때
- network를 통해 binary data를 주고 받을 경우
2.1.4 문자열의 표현
- C에서는 문자열을 맨 뒤에 null로 끝나는 character들의 배열로 간주한다.
- 각 문자는 표준 인코딩에 의해 표현 → 가장 흔한 것은 ASCII
- text data는 binary data보다 플랫폼으로부터 독립적임 (모두 같은 결과를 가질 것)
- byte ordering에서 독립적
- word size convention으로부터 독립적
- ASCII와 Unicode, 그리고 UTF-8
2.1.5 코드의 표현
int sum(int x, int y)
{
return (x + y);
}
위 코드가 서로 다른 머신에서 컴파일될 경우 이는 다음과 같은 기계어 코드로 표현된다.

같은 코드라도 여러 머신에서 다르게 표현되며, 이들은 호환 불가이다.
- instruction과 encoding이 다르기 때문
- instruction : 기계어 프로그램에서 사용하는 동작 지시
- encoding : 사용자가 입력한 언어, 기호 등을 컴퓨터가 이해할 수 있는 신호로 만드는 것
- 같은 프로세서라도 OS가 다르면 이에 따라 coding convention이 달라짐
2.1.6 Boolean algebra
- ~, &, |, ^
- ~ : NOT
- & : AND
- | : OR
- ^ : XOR
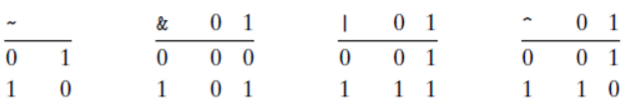
- bit 단위의 연산들이다.
비트 벡터(bit vector)
- 길이 w ( > 0)의 1과 0으로 이루어진 벡터
- ex) a = [0110], b = [1100] (w = 4) 일 때
- a | b = [1110]
- ~ b = [0011]
- a ^ b = [1010]
- a & b = [0100]
※ XOR의 성질
- (a^b)^a = b (순서를 바꿔보면 이 식이 성립함을 알 수 있다)
- 아래에서 예를 들어 확인해 볼 것
불 연산을 통해 집합 연산하기
A ⊆ {0, 1, . . . ,w− 1} 이고, 비트벡터 [a_{w-1} , ... , a_{1}, a_{0}] 에 대해
i ∈ A 일 때 a_{i} = 1 이라고 한다면
집합 A = {0, 3, 5, 6} 는 비트 벡터 a = [01101001] 로,
집합 B = {0, 2, 4, 6} 는 비트 벡터 b = [01010101] 로 나타낼 수 있다.
(즉, 집합의 원소를 값 1의 인덱스로 하여 비트 벡터로 나타냄)
이 때, 교집합은 AND 연산으로, 합집합은 OR 연산으로 나타낼 수 있다.
A ∩ B = {0, 6} 이고 a & b = [01000001],
A ∪ B = {0, 2, 3, 4, 5, 6} 이고 a | b = [01111101]
2.1.7 Bit-Level Operations in C
- C언어는 bitwise boolean operation을 지원한다.
- XOR 연산을 활용한 swap함수
- 초기값이 각각 a, b라고 한다면
- step 1) *y = a ^ b
- step 2) *x = a ^ (a ^ b) = (a ^ a) ^ b = 0 ^ b = b
- step 3) *y = b ^ (a ^ b) = (b ^ b) ^ a = 0 ^ a = a
void swap(int *x, int *y) { *y = *x ^ *y; // step 1 *x = *x ^ *y; // step 2 *y = *x ^ *y; // step 3 } // 퍼포먼스가 향상되는 이점이 있는 것은 아니다.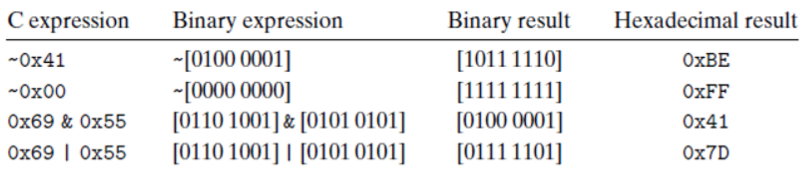
bit-masking
특정 마스크 비트를 원하는 비트에 연산하여 비트를 조작하는 테크닉이라고 보면 될 것 같다.
- ex) x = 0x89ABCDEF에서 최하위 바이트를 얻고자 할 때
- mask = 0xFF
- 0x89ABCDEF & 0xFF = 0x000000EF
- 예제 2.12 ) x = 0x87654321 일 때, 아래 결과를 도출해내고자 한다.
- 0x00000021
- 답) x & 0xFF
- 0x789ABC21
- 답) x ^ ~0xFF
- 0x876543FF
- 답) x | 0xFF
2.1.8 Logical Operations in C
- C언어는 ||, &&, ! 세가지의 논리 연산자를 제공한다.
bitwise operation VS logical operation
- logical operation에서는 0이 아닌 모든 것에 대해 true라고 1이라고 판단한다.
- logical operator를 0과 1에 대해서만 수행한다면 bitwise operation과 동일한 기능을 수행
- 단, bitwise operation에서는 short circuit evaluating이 없다

2.1.9 Shift Operations in C
- C언어는 shift operation(<<, >>)을 제공한다.
- 좌결합
- 왼쪽에서 오른쪽으로 수행하게 된다.
- x << j << k : x를 j bit만큼 왼쪽으로 shift & shift된 것에서 k bit만큼 왼쪽으로 shift
- (x << j) << k와 동일
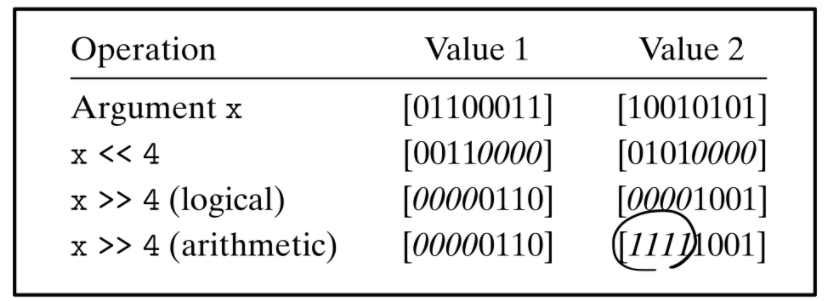
- x << k : x에서 k개의 bit만큼 왼쪽으로 이동, 빈공간은 0으로 채움
- logical : left-end를 k개의 0으로 채움
- arithmetic : left-end를 MSB와 동일한 것으로 k개를 채움, 이는 부호있는 수를 계산할 때 좋다.x >> k : x를 k개의 bit만큼 오른쪽으로 이동
- C표준에서 부호있는 수에 대해 어떤 right shift를 사용하는지 명확히 정의되지 않고 있다.
- 단지 대부분의 컴파일러에서 signed data에 대한 right shift를 arithmetic으로, unsigned data의 경우 logical로 처리한다.
'Computer Science > 컴퓨터 구조' 카테고리의 다른 글
| [CSAPP] 3.1 A Historical Perspective(역사적 관점) (0) | 2023.01.21 |
|---|---|
| [CSAPP] 2.4 Floating Point(부동소수점) (0) | 2023.01.19 |
| [CSAPP] 2.3 Integer Arithmetic(정수 연산) (0) | 2023.01.19 |
| [CSAPP] 2.2 Integer Representations(정수의 표시) (0) | 2023.01.19 |
| [CSAPP] Computer Systems A Programmer's Perspective: 컴퓨터 구조 책 추천 (0) | 2023.01.17 |
![[CSAPP] 2.1 Representing and Manipulating Information(정보의 저장)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdgZdtn%2FbtrWERmxxwY%2FkAL1kg9ldj1dPgkDKUkbi1%2Fimg.png)