6.4 Cache Memories(캐시 메모리)
초기 computer system에서의 memory hierarchies는 다음과 같았다.
- CPU registers - main memory - disk storage
하지만 여기서 CPU 와 main memory의 성능 격차가 커짐에 따라 다음과 같이 바뀌게 된다.
- CPU registers - small SRAM cache memories - main memory - disk storage

이렇게 CPU와 main memory 사이에는 작은 SRAM cache memory가 들어가게 된다.
SRAM cache memory
- L1 cache : CPU의 register file과 main memory 사이에 들어간다.
- register file과 같이 빠르게 접근 가능 → 약 4 cycle만에 접근 가능
- L2 cache : L1 cache와 main memory 사이에 들어간다.
- 약 10 cycle 만에 접근 가능
- L3 cache : L2 cache와 main memory 사이에 들어간다.
- 약 50 cycle 만에 접근 가능
아래에서는 한개의 L1 cache만 있는 memory hierarchy를 가정하고 살펴볼 것이다.
6.4.1 Generic Cache Memory Organization(기본 캐시 메모리 구조)

- 각 memory 주소가 m bit라면, 2^m = M개의 unique 주소를 가진다. → M을 기억하자.
- S개의 cache set들이 있으면, cache는 2^s = S개의 cache set들로 이루어진 배열을 갖는다. → S를 기억하자.
- ※ 여기서 승수로 올라가있는 s는 small s이고, set의 개수는 capital S이다.
- 각 cache set은 E개의 cache line을 갖는다. → E를 기억하자.
- 각 cache line에는
- 2^b = B bytes 크기의 cache block을 갖는다. → B를 기억하자.
- valid bit를 갖는다. ⇒ 해당 line이 의미 있는 정보를 가지는지 아닌지를 나타냄
- tag bit를 갖는다. ⇒ 현재 가지고 있는 주소의 일부분을 가져와 이 tag bit로 설정함(t = m - (b + s))
- cache의 capacity(총 size)는 $S \times E \times B$ bytes이다.
즉, cache는 (S, E, B, m)으로 정의가 가능하다.
예시
memory 주소 A를 load하라는 명령을 받음
→ 먼저 cache 로 A를 보내서 이 A word의 copy를 가지고 있는지를 확인
- 어떻게 확인할지는 아래에 언급 예정이다.
→ 만약 가지고 있다면, 이 word를 바로 CPU로 반환한다.
(b) 그림

m-bit짜리 주소를 나타내고 있다.
- cache 로 A를 보내서 이 A word의 copy를 가지고 있는지를 확인 ← 이 과정을 살펴볼 것이다.
- 우선 m bit 주소중에 s bit를 차지하는 Set index 값을 확인한다. 이 값으로 이 address를 가지는 word가 어떤 set에 저장되는지를 확인할 수 있다.
- 이후 t bit를 차지하는 Tag bit로 위에서 확인한 cache set에서 어떠한 cache line에 해당 word가 저장되는지를 확인한다.
- 이 때, tag bit가 matching이 되는 line이 있어도 valid bit가 0으로 설정되어 있다면, 이 해당 word를 현재 cache에 없다는 뜻이 된다.
- b bit를 차지하는 Block offset으로 해당 set의 해당 line에서 몇번째 offset에 이 word가 위치하는지를 알 수 있다.
💡 즉, cache에 address A를 가지는 word가 저장되어 있다는 것을 확인하기 위해 어떻게 동작할까?
- set index bit에 대한 cache set을 찾는다.
- tag bit와 매칭되는 cache line이 있는지를 위에서 찾은 cache set에서 확인한다.
- 매칭되는 tag bit가 있고 valid bit가 1로 설정되어 있을 경우, block offset bit를 통해 해당 cache line에 잇는 cache block에 해당 offset에 접근하여 address A를 가지는 word를 fetch한다.
- fetch한 word를 CPU로 반환한다.
연습문제 6.9

- 정답
- 256, 22, 8, 2
- 32, 24, 5, 3
- 1, 27, 0, 5
- 풀이
- C = S * E * $
- t = m - (b + s)
- S = 2^s
- B = 2^b
6.4.2 Direct-Mapped cached

E = 1, 즉 cache set 하나당 cache line이 하나만 존재하는 cache를 말한다.
- cache hit : load 하려는 word w의 복사본이 cache에 있을 때를 말함
- 바로 w word를 가지고 CPU로 반환 가능하다.
- cache miss : cache에 word w의 복사본이 없을 때를 말함
- CPU는 cache가 main memory로부터 word w를 포함하는 block을 복사하여 cache block에 저장하기까지를 전부 기다려야 한다.
- 이후 저장이 완료가 되면, cache block에서 word w를 추출하여 CPU로 반환한다.
- 아래부터는 여러 종류의 cache에서의 동일한 과정을 살펴볼 것이다.
- set selection
- lint matching
- word selection
- line replacement on misses
- conflict misses in direct-mapped caches
Set selection in Direct-Mapped Caches
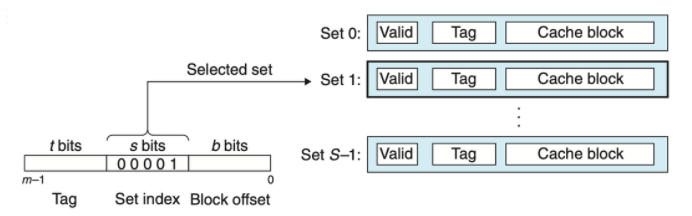
cache가 word w의 주소에서 중간에 위치한 set index bit를 해석한다.
- unsigned int로 해석
- 해당 bit를 해석한 값이 cache set의 index값이 됨
- ex) 00001(2진수)⇒ cache set의 index 1번(두번째 cache set)을 가리킨다.
Line matching in Direct-Mapped Caches

몇번 cache set인지는 위에서 구하였다. 따라서 이제는 word w가 이 cache set에 저장되어 있는지 아닌지를 살펴볼 예정이다.
- 해당 caceh set의 cache line의 valid bit가 설정되어 있고
- word w의 주소값에서의 tag bit와 위에서 구한 set의 cache line에 있는 tag bit가 같다면
해당 cache line에 word w가 저장되어 있다는 것이다. 이후 block offset bit로 cache block에서 시작 index를 찾아 word를 가져온다.
예시) 위에서는 tag bit가 0110이고, 이는 set i의 cache set에서의 tag bit와 동일하다. 또한 valid bit도 1로 설정되어 있으므로 block offset으로 word를 가져오려 한다.
- block offset이 100의 값을 가지고 있기 때문에, 이는 10진수로 해석하면 4가 되고, 이 4라는 값은 cache block에서 word w가 저장된 시작 index값이 된다.
- 이 때, 위 그림에선 word크기는 4-byte로 가정하고 있으므로 4 ~ 7번의 index에서 word w를 가져와 CPU로 반환한다(block에서 각 index가 차지하는 size는 1byte이다).
※ 만약 matching되는 tag bit가 없거나 valid bit가 0일 경우엔?? 아래의 설명을 마저 봐보자.
line replacement on misses
cache miss의 경우로는 다음이 있다.
- valid bit가 0일 경우
- tag bit가 매칭되는 cache line이 없을 경우
이때는 바로 하위의 memory에서 word w를 포함하는 block을 가져와 이 cache에 저장하게 된다. 여기서 word가 아닌 block을 가져온다는 것을 인지하자. 이는 word의 크기 이상의 block을 말하는 것이고, cache block의 크기만큼 memory에서 가져오는 것이다.
만약 다음의 경우엔 어떻게 해야 할까?
- cache miss임과 동시에 모든 cache line의 valid bit가 1로 설정되어 있다면?
이 경우에는 victim이 생기게 된다. ⇒ 즉, cache에서 나가게 되는 block이 생긴다는 것.
이 때 어떠한 cache line을 희생시킬 지를 정하는 replacement policy가 cache마다 있을 텐데, 이 direct mapped cache의 경우에는 set 안에 line이 하나뿐이여서 그냥 교체하면 된다.
Simulation
CPU가 read를 연속적으로 수행하는 것을 시뮬레이션 해보자.
조건
- CPU가 한번에 읽는 word의 크기는 1-byte로 가정한다.
- 처음 cache는 비어있다고 가정하자.

- 각 row는 cache line을 나타낸다.
- 맨 왼쪽 column은 set의 index를 의미한다.
- set index bit : 2-bit (0 ~ 3의 cache set을 가짐)
- 나머지 4개의 column은 실제 cache set에 있는 데이터들을 의미한다.
- valid bit : 1-bit
- tag bit : 1-bit (tag bit는 1-bit임을 알 수 있다)
- cache block : 2-byte (block index bit는 1bit임을 알 수 있다)
- 위의 정보를 통하여 address는 총 4-bit크기로 표현 할 수 있다(즉, 주소는 0 ~ 15사이의 값을 가진다).
시뮬레이션
- 1.주소 0에서 word를 읽어오는 명령을 CPU가 실행한다.
- 우선 cache를 살필 것이다.
- 주소 0에서 set index는 0임을 알 수 있다. 따라서 cache set 0번을 살펴본다.
- valid bit가 0으로 설정되어 있다. → cache miss 발생!
- cache는 하위 memory(여기서는 main memory)에서 block 0을 fetch 해온다.
- → (이 때 word의 크기는 1-byte 이지만, block은 2-byte크기 이므로, 주소 0에 있는 word와 1에 있는 word를 포함하는 block을 fetch한다)
- 그리고 0번 cache set의 cache block에 fetch한 block을 저장한다.

- 저장한 m[0]을 block[0]으로부터 CPU로 반환한다.
- 2.주소 1에 있는 word를 읽는 명령을 실행한다.
- 위에서 주소 1 block도 같이 fetch 해왔다. → cache hit!
- 바로 CPU로 해당 block[1]에 있는 m[1]을 반환한다.
- 3.주소 13에 있는 word를 읽는 명령을 실행한다.
- 먼저 cache에서 주소 13을 가지는 word가 저장되어 있는지를 확인한다.
- 주소 13을 bit표현 해보면 다음과 같다. → 1101(2진수)
- tag bit(1), set index bit(10), block offset bit(1)
- 따라서 2번 cache set을 찾아봤더니 valid bit가 0이다. → cache miss!
- 이 때, 12번과 13번 주소의 word 두개를 포함하는 block을 fetch하여 저장한다.cache는 하위 memory에서 주소 13을 포함하는 block을 fetch하여 저장한다.

- 주소 13번의 word m[13]을 block[1]에서 가져와 CPU로 반환한다.
- ⚠️ 왜 13번 주소를 가지는 m[13]이 block[1]에 저장되었을까?⇒ 즉, block[1]에 저장되는 word가 바로 13번 주소를 가지는 word m[13]이라는 뜻.
- ⇒ 따라서 m[13]을 두번째로, 그리고 그 앞에 있는 12번 word를 같이 가져와 block[0]에 저장하게 된 것이다.
- ⇒ block offset bit가 1이다.
- 4.주소 8번에 있는 word를 읽는 명령을 실행한다.
- 8번의 주소를 해석하면 다음과 같다. → $[1][00][0]_2$.
- tag bit(1), set index bit(00), block offset bit(1)
- 0번의 cache set을 찾아보니 valid bit가 1로써, 먼저 들어가 있는 cache가 있었다 → cache miss!
- cache line이 하나 뿐이므로 이미 들어가있는 cache block을 8번과 9번 word로 교체하게 된다.
- 8번의 주소를 해석하면 다음과 같다. → $[1][00][0]_2$.

-
- 이후 block[0]에 있는 m[8] word를 CPU로 반환한다
- 5.다시 0번 주소의 word를 읽는 명령을 실행한다.

-
- 위와 마찬가지로 replacement가 발생하게 된다.
- 이렇게 같은 set에 대해 alternating이 발생하는 것을 conflict miss라고 한다.
Conflict Misses in Direct-Mapped Caches

위의 코드를 실행했을 경우 어떤 상황이 발생하는 지를 살펴보자
⇒ (쉽게 생각하기 위해 block의 크기를 16bytes, 그리고 set을 2개 있는, 총 32bytes의 cache size를 가진다고 가정해보자). 두번째 사진과 같이 cache에 저장된다고 할 때 몇번의 실행 과정을 보자면,
- x[0]을 read한다. ⇒ cache miss! ⇒ set index가 0 ⇒ cache에 16-byte block을 저장한다(x[0] ~ x[3])
- y[0]을 read한다. ⇒ cache miss! ⇒ set index가 0 ⇒ conflict miss! ⇒ 16-byte block을 저장한다(y[0] ~ y[3])
이렇게 매 루프마다 16byte의 block을 fetch하고 저장하고 replace되는 과정이 일어난다. 이렇게 같은 cache set에 반복적으로 load & evit(희생)이 일어나는 것을 “thrasing” 이라고 한다.
💡 이러한 thrasing은 2의 제곱수의 배열을 번갈아가며 참조할 때 발생하기 쉬운 것을 알 수 있다. 왜냐하면 x[7] 다음에 바로 y[0]이 연속적으로 메모리 상에 위치하게 되는데, 이러한 이유로 set index가 동일하게 되는 경우가 발생할 확률이 올라가기 때문이다.
그럼 어떻게 thrasing을 해결할 수 있을까? ⇒ 굉장히 쉽다고 한다. 이는 바로 위의 callout에서 언급했듯, 2의 제곱수로 크기를 설정하는 것이 아닌 x[8]대신 x[12]로 선언하게 된다면, 다음과 같이 cache에 저장되게 된다.

즉, x[0]과 y[0]을 참조할 때, 서로 다른 cache set에 저장되므로 conflict miss가 발생하지 않을 것이고, 이에 thrasing을 예방할 수 있다.
생각해보면 좋은 것 - 왜 set index bit가 address의 중간에 위치할까?
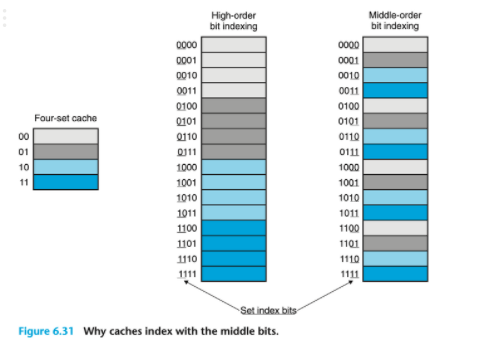
주소가 4-bit로 표현되는 0 ~ 15사이의 값을 주소값으로 갖는 것을 생각해보자.
⇒ cache set의 크기는 set의 크기를 4로 하게 되면, set index bit는 2-bit 크기를 가진다.
⇒ 이 때, set index bit가 주소값에서의 상위 2-bit에 위치한다고 가정해보자.
⇒ 위의 그림에서와 같이 연속된 4개의 주소가 같은 cache set에 위치할 것임을 알 수 있다.
⇒ program이 좋은 spatial locality를 가지고 있고, 배열의 요소들을 순서대로 순서대로 scan한다고 할 때, 첫 4개의 요소들은 cache에 공간이 넓어 하나씩 차지해도 될 것을 한개의 set을 두고 경쟁하는 꼴이 된다.
⚠️ 이 때, 나는 처음에 어차피 처음부터 끝까지 scan한다고 하면, cache miss되는 횟수는 동일하지 않을까 하는 생각에 왜 더 손해인지 헷갈렸었다. 이는 다음의 예시를 보고 조금 더 확실히 알게 되었다.
💡 Practice Problem 6.11 high-order s bit에 set index bit가 위치하는 어떠한 주소 시스템을 사용하는 가상의 cache가 있다고 해보자. 이러한 cache의 경우 연속된 memory block들의 덩어리가 같은 cache set에 매핑된다.
A. 그럼 몇개의 연속된 배열의 chunk가 같은 cache set에 매핑되는가? ⇒ block offset bit가 없을 경우(block이 한칸짜리인 경우) 2^t 개의 연속된 memory chunk들이 하나의 set에 매핑된다. ⇒ 왜? address를 구성하는 bit가 s와 t뿐일 때, s가 같은 것의 bit패턴의 수는 나머지 t-bit로 표현할 수 있는 것의 개수만큼 있기 때문.
B. int형 array[4096]을 0부터 4095까지 차례대로 참조할 때, 어느 시점이던간에 cache에 저장되는 최대 array block들의 수는? 이 때, (S, E, B, m) = (512, 1, 32, 32)의 cache로 가정한다. ⇒ cache의 capacity로는 512개의 32byte block들이 있다. 이 때, tag bit의 크기는 18이므로, 총 2^18개의 연속된 memory chunk가 하나의 cache set에 매핑되는 것을 알 수 있다. ⇒ 현재 4096크기의 배열을 참조하고 있는데, 이 경우에는 4096이 2^18보다 작기 때문에 하나의 cache set 0번에 전부 매핑된다. ⇒ 이렇게 된다면, cache는 딱 하나의 array block(8개의 chunk, 32byte)만이 최대로 저장되는 개수가 된다. ⇒ 이렇게 남은 cache set의 용량이 많은데도 불구하고, 조금의 공간에 저장하게 되면서 cache를 비효율적으로 사용하고 있음을 알 수 있다.
6.4.3 Set Associative Caches
direct-mapped cache에서의 근본적인 문제는 딱 하나뿐인 cache line에서 온다. 이에 set associtve cache는 하나의 cache set에 1 < E < C/B 개의 cache line을 가지도록 하며, 이러한 것을 E-way set associative cache라고 부른다.

위 그림에서와 같이 cache line수가 2인 2-way set associative cache를 살펴볼 예정이다.
Set Selection in Set Associative Caches

direct-mapped cache와 동일하다.
Line Matching and Word selectionin Set Associative Caches

associative memory
먼저 associative memory에 대해서 살펴보면 다음과 같다.
- 기존 memory는 주소를 input으로 주어 값을 반환한다.
- associative memory라는 것은 key를 input으로 하여 value를 반환한다.
왜 associative memory라는 것을 언급하는 건가? → set associative cache에서의 각 set들을 작은 associative memory라고 생각할 수 있기 때문이다.
- key : tag와 valid bit
- value : block의 content
direct-mapped cache에서의 line matching과 차이점
- direct-mapped cache에서는 cache set만 정해지면 들어갈 cache line이 정해져 있다(line이 set당 하나밖에 없으므로)
- 하지만 set associative cache에서는 어떤 set인지만 구하면, 그 안의 어느 line이던간에 전부 들어갈 수 있다.
- 즉, word를 가져올 때에는 위에서 설명한 associative memory에서와 같이 key를 이용해 block에 있는 원하는 word를 가져올 수 있다.
Line Replacement on Misses in Set Associative Caches
cache miss가 발생했는데, 모든 line이 꽉 다 차있기까지 한다? ⇒ 어떤 것을 replace해야 하지?
이러한 상황에서 victim을 정하기 위해 replacement policy를 가지고 있다.
Replacement policy
- 가장 간단한 policy : random하게 대체 될 line을 고른다.
- LFU(Least Frequentyl used) : 과거에 제일 적게 참조된 것을 replace
- LRU(Least recently used) : 가장 최근에 참조된 시점이 가장 과거인 것을 replace
이러한 정책들 모두 추가적인 CPU시간과 하드웨어 unit들을 필요로 하게 된다. 하지만 하위 cache및 main memory에서는 cache miss가 더 비용이 비싸지기 때문에 이러한 replacement policy를 적용하는 것이 더 좋다.
6.4.4 Fully Associative Caches
위에서 봤던 set associative caches에서 특수화된 case를 말한다. 이 때, 특수화된 case는 E = C/B 를 말한다.

즉, cache는 오직 한개의 set만을 가지고, 이 한개의 set안에 cache의 모든 cache line이 포함되는 구조를 말한다. 여기서도 마찬가지로 위와 같이 cache에서의 작동을 살펴볼 예정이다.
Set Selection

이 fully associative cache의 경우 set selection은 지나쳐도 좋다.
Line matching and word selection

set associative cache와 동일하게 line matching을 수행한다.
단, 이 경우에는 small cache에 주로 사용되는 방식이다. 이는 cache 회로가 병렬적으로 매칭되는 tag들을 탐색해야 하고, 이럴 경우 크고 빠른 associative cache를 만들기란 어렵고 비싸다. 따라서 작은 size의 cache에 적합하다.예) TLB(Translation Lookaside Buffer - virtual memory system에서 쓰임, 9단원에 나옴)
6.4.5 Issues with Writes(쓰기와 관련된 이슈)
read에서는 cache에서 동작하는 과정들이 꽤나 분명했다. 하지만 write에서는 그렇지 않은 점들이 있는데 이에 대해 살펴보려고 한다.
이미 cache에 저장되어 있는 word w에 write를 수행하려고 한다면(write-hit 상황)
- write-through : 매 write마다 cache에서 word w를 update한 후 그 하위 memory에 있는 word w까지 update한다.
- 장점 : 간단하다.
- 단점 : bus traffic을 유발한다.
- write-back : 오직 replacement 알고리즘에 의해 cache 에서 희생될 때에만 lower memory에 해당하는 word w를 update한다.
- 장점 : bus traffic을 매우 줄여준다.
- 단점 : 복잡성이 증가한다. cache는 현재 cache line의 block이 변경되었는지에 대한 정보를 담는 추가적인 “dirty bit”를 유지해야 한다.
write-miss인 상황에서는
- write-allocate : write할 word를 포함하는 block을 load한다(기존 read와 동일). 그리고 cache block에 저장한 후 이 block을 update한다.
- 공간 지역성을 착취하려는 방법
- 주로 write-back을 수행하는 cache에서 이를 이용한다.
- no-write-allocate : cache를 지나치고 바로 lower memory에 접근해서 직접 update를 수행한다.
- 주로 write-through를 수행하는 cache에서 이를 이용한다.
주로 write-back, write-allocate cache를 채용하기를 제안한다
- lower level에 있는 cache들이 보다 선호하는 방식이다.
- write-through방식이 더 큰 전송 시간을 야기하기 때문이다.
- 이러한 이유로 virtual memory system에서는 write-back 방식만을 사용한다.
- 그럼 복잡성이 증가하는 문제는? ⇒ 하지만 이 복잡성은 logic(회로)의 밀도가 향상됨에 따라 큰 문제가 되지 않게 되었다.
- write-back, write-allocate 접근법은 read가 다뤄지는 방식과 대칭적이다.
- 둘 모두 locality를 착취한다.
6.4.6 Anatomy of a Real Cache Hierarchy(실제 캐시 계층구조의 해부)
지금까지 cache가 오직 program data만을 들고 있는 것을 가정해왔다. 지금부터는 instruction도 들고 있는 것들을 포함하여 여러 cache의 분류를 살펴볼 것이다.
- d-cache
- program data만을 들고 있는 cache를 말한다.
- i-cache
- instruction만을 들고 있는 cache를 말한다.
- unified cache
- 둘 모두를 가질 수 있는 cache를 말한다.
- 그럼 modern processor는 어떠한 cache를 가지고 있을까?
- ⇒ 이렇게 i와 d 각각 분리된 cache를 갖고 있다. 이유는 다음과 같다.
- instruction과 data를 동시에 읽어올 수 있다.
- 각각의 접근 패턴이 달라, 이에 따라 각각을 최적화할 수 있다.
- block size, associativity, capacity 등에 대해 최적화 가능
- data 접근을 했을 경우, i-cache에서 conflict-miss를 발생시키지 않는다. 분리되었을 경우, 다른 cache에 영향을 주지 않는다는 뜻

- ⇒ 이렇게 i와 d 각각 분리된 cache를 갖고 있다. 이유는 다음과 같다.
6.4.7 Performance Impact of Cache Parameters(캐시 매개변수의 성능에 대한 효과)
cache의 성능을 나타내는 지표들을 살펴볼 것이다.
- miss-rate : miss가 발생한 횟수 / 참조한 횟수
- hit-rate : 1 - miss-rate
- hit-time : cache에서 CPU까지 word가 전달되는 시간
- set selection + line selection + word selection
- L1 cache의 경우 수 clock cycle이 걸림
- miss penalty : cache miss로 인해 추가로 드는 시간
- L1 cache에서의 miss → L2에서 가져옴 : 약 10 cycles
- L2 : 약 50 cycles
- L3 : 약 200 cycles
Impact of Cache Size
cache size가 클수록 hit-rate가 증가한다.
⇒ 그러나 hit-time이 증가한다.(CPU가 cache로부터 요청한 word를 반환받기까지의 시간 - 성능과 직결)
⇒ 왜 size가 클수록 hit-time이 증가하는가? 위에서 언급했다시피, size가 클수록 tag들을 매칭하는데에 시간이 더 걸린다고 한다. 만약 block size가 크다면, miss가 발생했을 시에 load하는 block의 크기가 크므로 이에 따른 transfer time이 증가하게 될 것이다. 따라서 hit-time이 증가하게 될 것(내 뇌피셜..).
⇒ 따라서 L1의 cache size가 하위 계층의 memory보다 더 작은 것이다.
Impact of Block Size
spacial locality를 착취하여 hit-rate를 향상시킨다.
⇒ 하지만, 동일한 cache size에 block size가 더 크다는 뜻은 cache line의 개수가 더 작다는 것을 뜻한다.
⇒ 이렇게 되면, temporal locality가 spatial locality보다 더 잘 착취되는 프로그램에선 hit-rate를 더 악화시킬 수 있다.
⇒ Modern processor는 cache block을 64-byte크기로 타협을 봤다.
Impact of Associativity
장점 : cache thrasing에 대한 취약성을 줄일 수 있다(direct-mapped cache의 conflict miss의 문제점을 완화시키기 위해 set associative cache를 살펴봤었다).
단점
- 구현하기 비싸다.
- 빠르게 만들기 어렵다.
- 각 line마다 tag bit를 더 필요로 하기 때문이다.
- 추가적인 LRU bit가 line마다 추가되어야 한다.
- 이를 컨트롤 할 수 있는 추가적인 control logic이 필요하다.
- hit-time이 증가한다 ⇒ 복잡성이 증가했기 때문
- miss penalty 증가 ⇒ replace하는 알고리즘 등으로 인해 복잡성이 증가했기 때문에
보통 높은 성능의 system에선 L1 cache엔 smaller associativity를, 그 아래 하위 memory에선 보다 higher associativity를 사용한다고 한다.
- L1과 L2에선 : 8-way set associativty
- L3에선 : 16-way set associativity
'Computer Science > 컴퓨터 구조' 카테고리의 다른 글
| [CSAPP] 6.6 Putting It Together: The Impact of Caches on Program Performance(프로그램 성능에 대한 캐시의 영향) (0) | 2023.02.15 |
|---|---|
| [CSAPP] 6.5 Writing Cache-Friendly Code(캐시 친화적 코드 작성) (0) | 2023.02.15 |
| [CSAPP] 6.3 The Memory Hierarchy(메모리 계층구조) (0) | 2023.02.10 |
| [CSAPP] 6.2 Locality(지역성) (0) | 2023.02.09 |
| [CSAPP] 6.1 Storage Technologies(저장장치 기술) (0) | 2023.02.09 |
![[CSAPP] 6.4 Cache Memories (캐시 메모리)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F9mA0C%2FbtrYSN8jrkO%2FPqov9wN6qsgDe3Ks1B9aRK%2Fimg.png)