[회귀분석] 회귀모형의 진단과 수정 -1

부터 재생00:59

부터 재생03:37

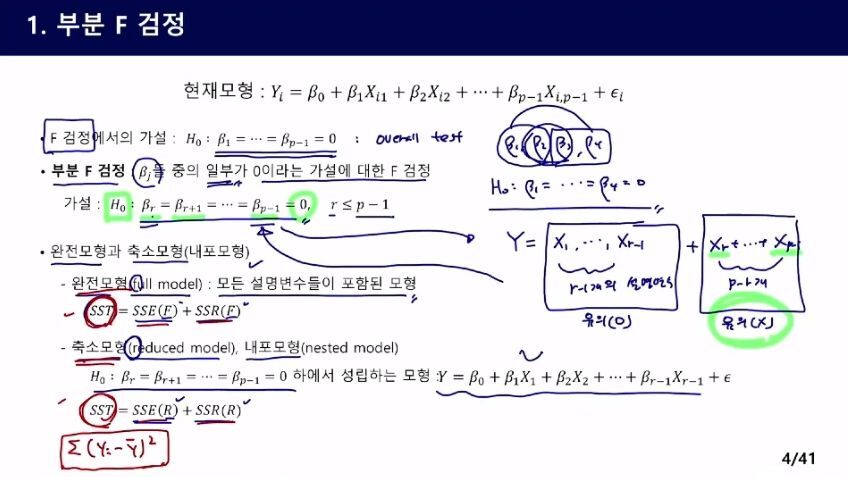
부분적으로 회귀 검정을 할 수 있다.

SST는 완전모형이나 축소모형이나 동일하다. SST에는 회귀식이 들어있지 않기 때문이다.

부터 재생09:06

Bold 글씨체는 벡터다! scalar와 구별 잘하기

축소한 모형과 완전 모형을 비교해서 축소 모형의 큰 차이가 없으면 축소 모형을 선택하면 된다.

부터 재생13:12

설명변수가 많은 수록 y의 fitting 값이 y에 가까워 진다. (Y(hat)의 식만 봐도 알 수 있죠) 따라서 full model의 SSE가 더 작고 SSR이 크다.

두 모형의 SSE, SSR의 차이를 비교하면 된다.

부터 재생19:07

예제

부터 재생21:51

부터 재생23:56

H0를 기각할 수 없다.

즉 필요 없는 변수라는 것(귀무가설 기각 못함 = 채택)

부터 재생27:28

개별 T검정과 F검정이 같다.

부터 재생33:14

예제 축자 검정

B0에서 B0 + B1로 추가되었을 때 3314.6만큼 변했다는 것을 의미. 즉 영향이 크다. 따라서 해당되는 P value도 유의하다

부터 재생36:37

부터 재생40:12

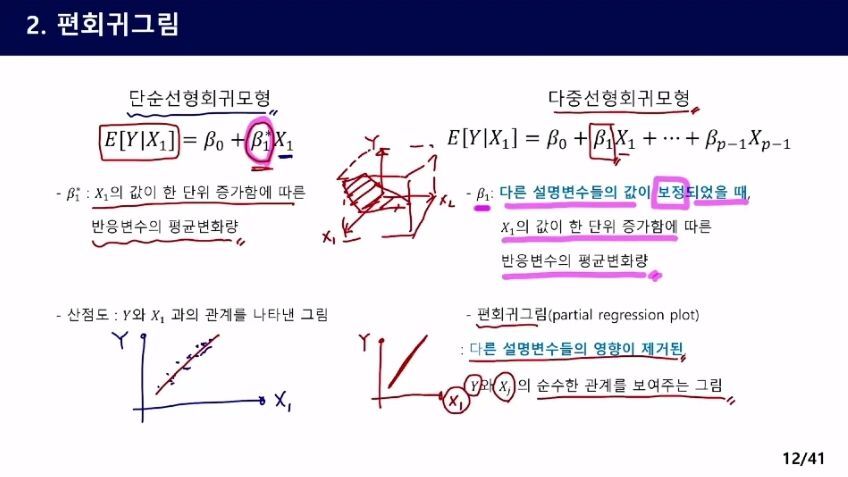
절편과 기울기가 모두 달라진다. 영향을 제거해버리기 때문에. 나머지 변수들을 보정한 것이 아니고 제거한 것이다.

부터 재생42:29

x1을 반응변수 x2, x3를 설명변수로 만들면 x2와 x3의 영향을 제거할 수 있다.

잔차의 개념이기 때문에 (0,0)을 지난다.ㅍ

편회귀상관계수의 기울기가 B1 값이 된다.

부터 재생48:39

예제

부터 재생51:02

수평

B1(HAT)이 0에 근사할 때 분모의 경우(분모가 큰 경우) X2와 X3가 X1에 영향을 주지 못한다는 것이고 분자의 경우(분자가 작은 경우) X1,X2에 의해 Y가 설명이 대부분 된다는 것.

수직

위에서 반대

X1은 중요한 변수다.

부터 재생55:04

적합결여검정

부터 재생56:11

그림을 이용한 적합결여검정

부터 재생58:07

부터 재생01:02:30

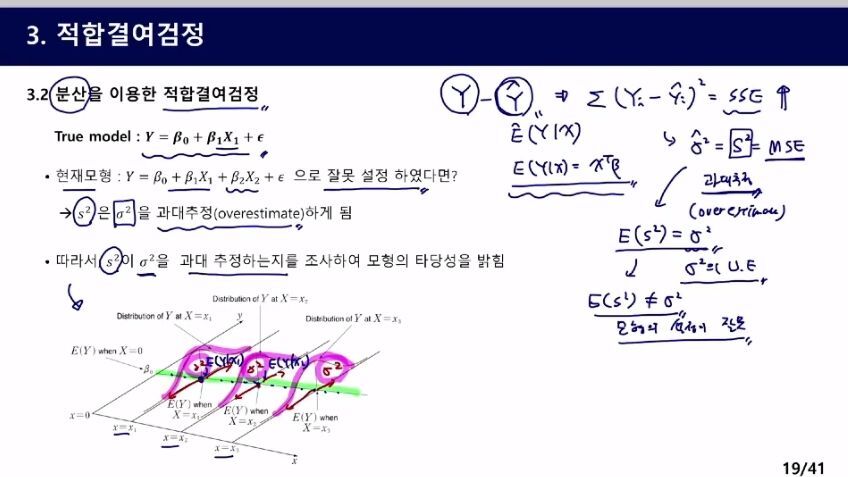
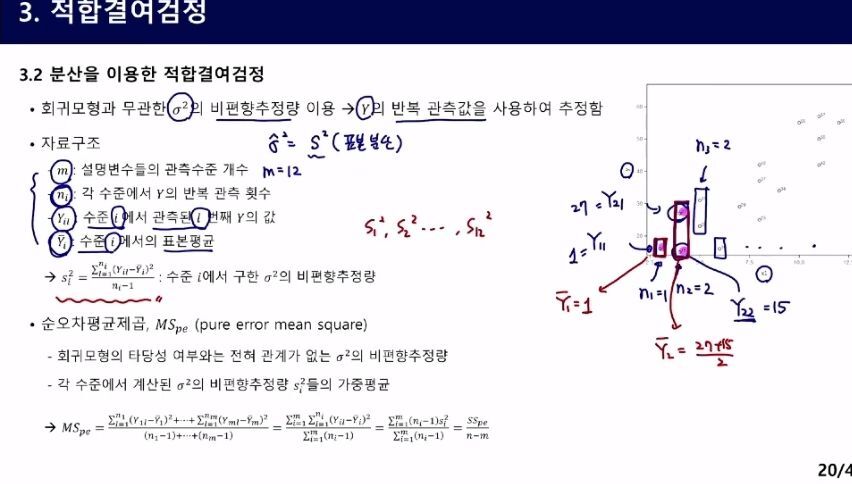
비편향추정량을 만족하는지 확인해서 과대추정 여부를 조사한다.

그림에서 현재 등분산성을 만족한다고 가정. 분산이 모두 같다.

부터 재생01:05:16

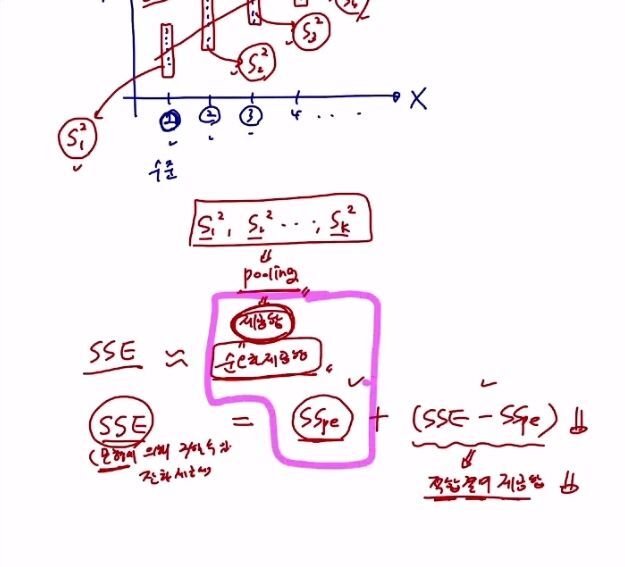
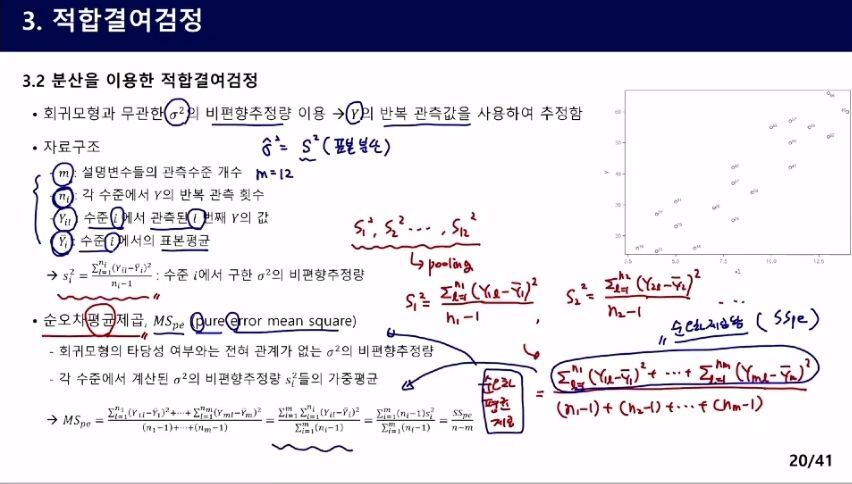
pooling은 합친다.

SSE(모형에 의해 구할 수 있는 잔차 제곱합)

적합결여제곱합이 작을 수록 좋다.

부터 재생01:08:19

순오차제곱합 구하는 법

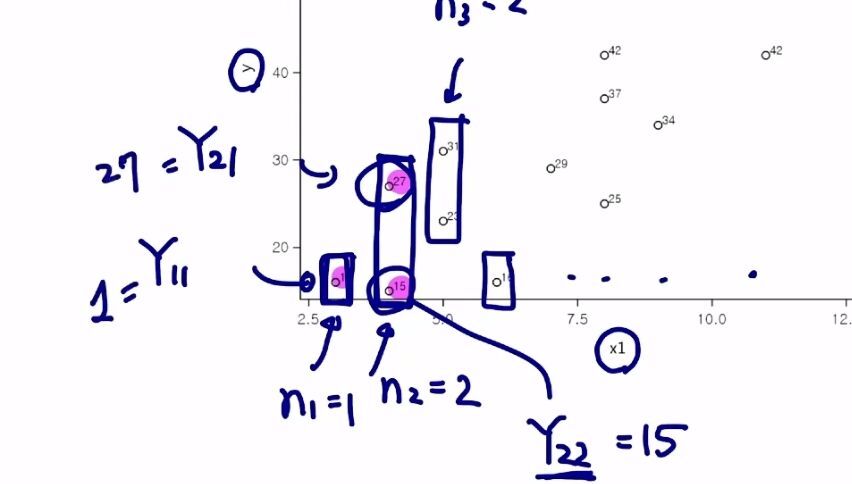
부터 재생01:11:25

부터 재생01:12:44

부터 재생01:15:21

부터 재생01:16:29

부터 재생01:16:26

n-m의 카이제곱분포를 따른다는 것은 증명을 하지 않을 것. 그냥 알고 있기.

각 수준의 표본오차 각각 구하기

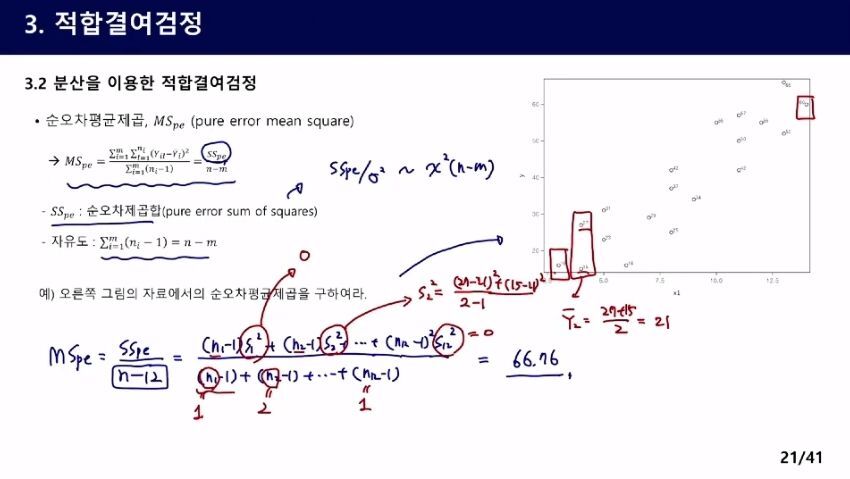
부터 재생01:19:54

적합결여제곱합: SSE를 SSpe로 설명하지 못한 부분

부터 재생01:24:48

예제

1번

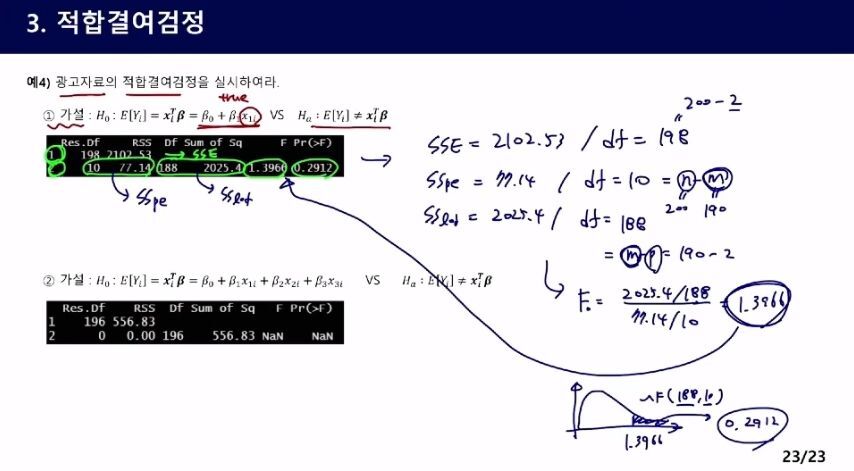
부터 재생01:28:16

2번

자유도가 0이라는 것은 두 개이상 반복된 것이 없다는 의미. 다 서로서로 반복 측정된 것이 없고 따로 측정되었다는 것

이럴 때는 소수점 별로 측정된 측도를 자연수로 바꿔서 중복되게 만드는 방법이 있다.

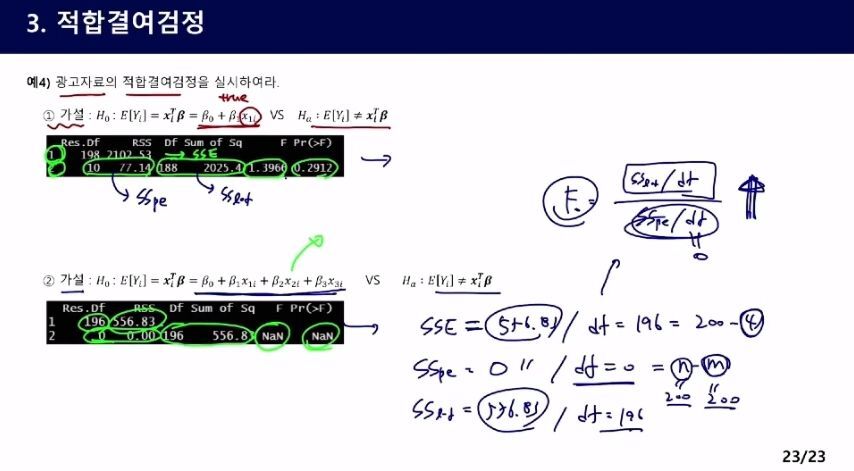
부터 재생01:31:04