[회귀분석] 중회귀분석에서의 적합도와 분산분석

자유도 부분에서 p는 회귀계수의 개수이고 SSR의 자유도는 SST와 SSE의 차로 구해진다. 딱히 이유는 없다.

예제

적합도

S가 작을 수록 좋다.

자유도로 나눠주는 이유는 SSE는 설명변수의 개수가 증가할수록 감소하기 때문이다. 설명하지 못하는 설명변수가 들어감에도 개수가 늘어난다고 SSE가 감소하면 좋지 않기 때문이다. 따라서 자유도로 나누어주는 것이다.

이에 대한 추가 설명

설명변수가 3개였을 때 100이였는데 2개 추가해서 98.2이면 추가된 설명변수의 영향이 크지 않다는 것.

따라서 추가된 설명변수의 영향을 잘 파악하기 위해 n - p(설명변수의 개수)로 나눠줘야 함.

SSE는 변동이 있기 때문에 보정된 결정계수를 이용한다.

예측도 및 F 검정

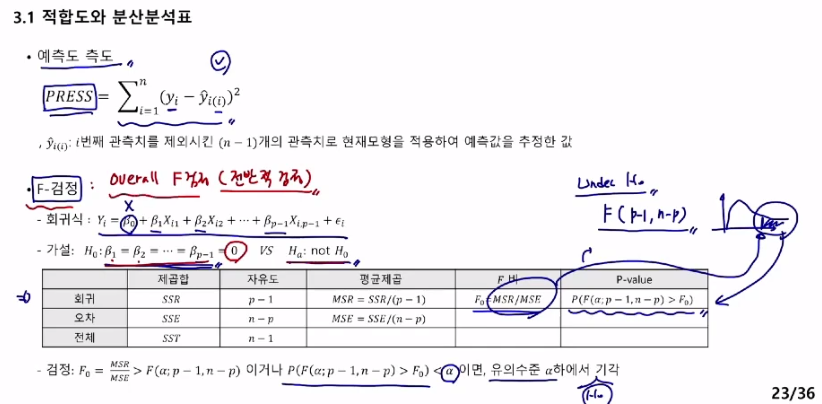
예제

귀무가설 기각

쿼드라틱 폼(이차형식)

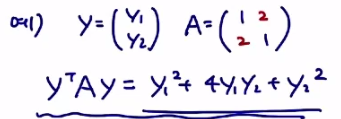
1. 총제곱합 SST의 이차형식

2.오차제곱합 SSE의 이차형식

3. 회귀제곱합 SSR의 이차형식

제곱합의 이차형식 매트릭스 표현은 랭크를 구하는 등의 계산을 용이하게 해준다.

멱등행렬의 대각원소의 합(trace) tr(A)는 rank가 된다.

A가 멱등행렬이면 tr(A) = rank(A)

y와 곱을 함으로써 선형결합을 이루고 이루는 공간을 랭크이고 자유도의 의미와 동일하다.

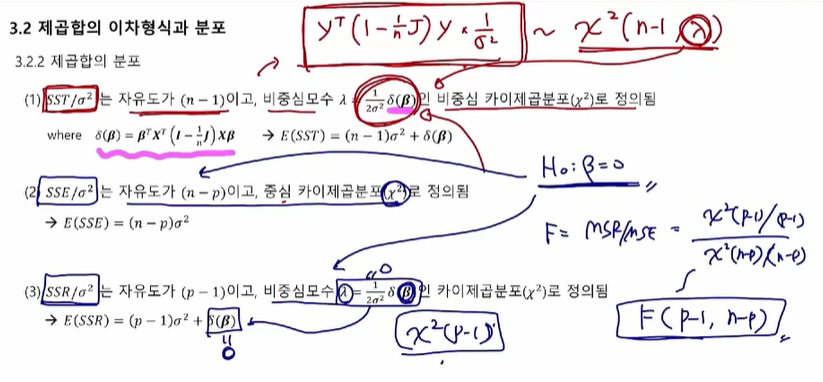
제곱합의 분포

귀무가설 H_0 : B =0이라는 가정 하에서는 중심 카이제곱분포를 따르게 된다.

중회귀분석에서의 추론

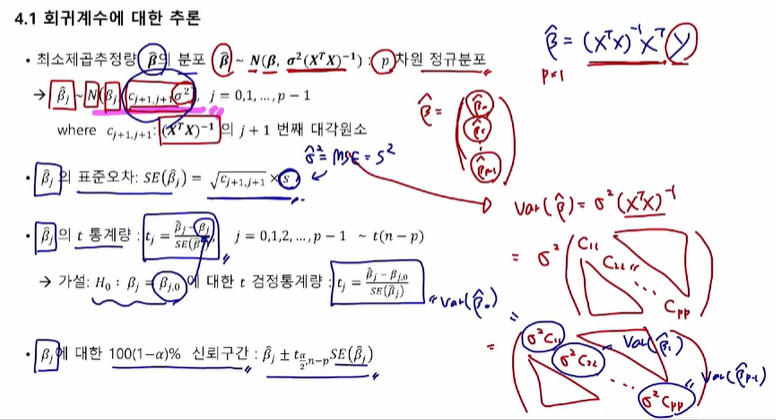
회귀계수에 대한 추론

예제

3차원

귀무가설 기각

귀무가설 채택 불가

각 회귀계수에 대한 95% CI

신뢰구간이 0을 포함하고 있으면 회귀식이 유의하지 않다.

반응변수의 평균에 대한 추정

반응변수의 평균에 대한 예측

예제

회귀절편에 해당하는 1 (항상 1로 고정)

B, S 등은 앞에서 다 구함

예측 구간은 오차항을 포함하기 때문에 1+ 추가

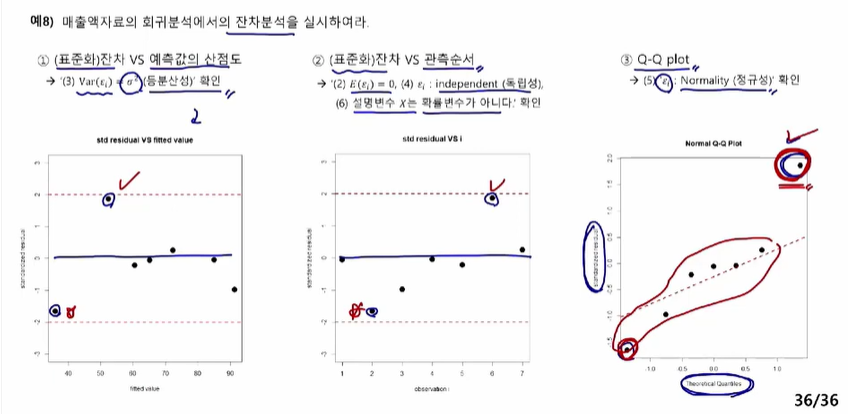
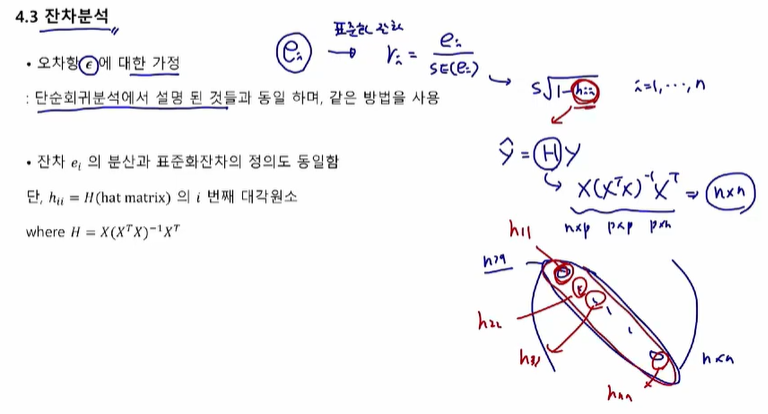
잔차분석

예제